【题目】(本题满分13分)已知函数![]() ,
,![]() .
.
(Ⅰ)求函数![]() 的最小正周期与单调增区间;
的最小正周期与单调增区间;
(Ⅱ)求函数![]() 在
在![]() 上的最大值与最小值.
上的最大值与最小值.
参考答案:
【答案】(1)![]() ,增区间为
,增区间为![]() ;(2)最小值
;(2)最小值![]() ,最大值
,最大值![]() .
.
【解析】
试题分析:本题主要考查倍角公式、两角和的正弦公式、三角函数的周期、单调区间、三角函数的最值等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,先利用倍角公式和降幂公式以及两角和的正弦公式化简表达式,使之成为![]() 的形式,利用
的形式,利用![]() 计算周期,再利用
计算周期,再利用![]() 的函数图象解不等式,求出单调递增区间;第二问,将已知x的取值范围代入表达式,结合图象,求三角函数的最值.
的函数图象解不等式,求出单调递增区间;第二问,将已知x的取值范围代入表达式,结合图象,求三角函数的最值.
试题解析:![]()
![]()
![]() .
.
(Ⅰ)![]() 的最小正周期为
的最小正周期为![]()
令![]() ,解得
,解得![]() ,
,
所以函数![]() 的单调增区间为
的单调增区间为![]() .
.
(Ⅱ)因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
于是 ![]() ,所以
,所以![]() .
.
当且仅当![]() 时
时 ![]() 取最小值
取最小值![]()
当且仅当![]() ,即
,即![]() 时最大值
时最大值![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
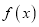 是定义在D上的函数,若对D中的任意两数
是定义在D上的函数,若对D中的任意两数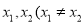 ),恒有
),恒有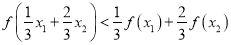 ,则称
,则称 为定义在D上的C函数.
为定义在D上的C函数.(1)试判断函数
 是否为定义域上的C函数,并说明理由;
是否为定义域上的C函数,并说明理由;(2)若函数
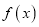 是R上的奇函数,试证明
是R上的奇函数,试证明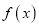 不是R上的C函数;
不是R上的C函数;(3)设
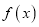 是定义在D上的函数,若对任何实数
是定义在D上的函数,若对任何实数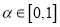 以及D中的任意两数
以及D中的任意两数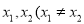 ),恒有
),恒有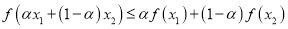 ,则称
,则称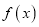 为定义在D上的π函数. 已知
为定义在D上的π函数. 已知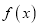 是R上的π函数,m是给定的正整数,设
是R上的π函数,m是给定的正整数,设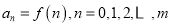 ,且
,且 ,记
,记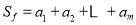 . 对于满足条件的任意函数
. 对于满足条件的任意函数 ,试求
,试求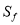 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】以A表示值域为R的函数组成的集合,B表示具有如下性质的函数
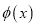 组成的集合:对于函数
组成的集合:对于函数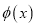 ,存在一个正数M,使得函数
,存在一个正数M,使得函数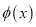 的值域包含于区间[-M,M]。例如,当
的值域包含于区间[-M,M]。例如,当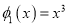 ,
, 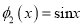 时,
时, 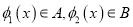 ,现有如下命题:
,现有如下命题:①设函数
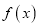 的定义域为D,则“
的定义域为D,则“ ”的充要条件是“
”的充要条件是“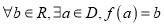 ”;
”;②若函数
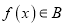 ,则
,则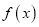 有最大值和最小值;
有最大值和最小值;③若函数
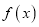 ,
, 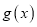 的定义域相同,且
的定义域相同,且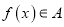 ,
, 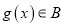 ,则
,则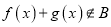
④若函数
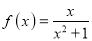 ,则
,则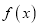 有最大值且
有最大值且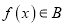 ,
,其中的真命题有_____________。(写出所有真命题的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分13分)已知数列
 的前
的前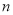 项和为
项和为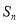 ,
, 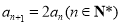 ,且
,且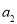 是
是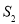 与
与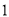 的等差中项.
的等差中项.(Ⅰ)求
 的通项公式;
的通项公式;(Ⅱ)若数列
 的前
的前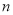 项和为
项和为 ,且对
,且对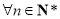 ,
,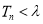 恒成立,求实数
恒成立,求实数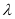 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
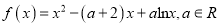
(I)若
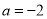 ,求曲线
,求曲线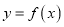 在
在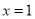 处的切线方程;
处的切线方程;(II)讨论函数
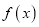 在
在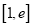 上的单调性;
上的单调性;(III)若存在
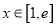 ,使得
,使得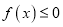 成立,求实数a的取值范围。
成立,求实数a的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的对称中心为原点O,焦点在x轴上,离心率为
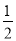 ,且点
,且点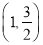 在该椭圆上。
在该椭圆上。(I)求椭圆C的方程;
(II)过椭圆C的左焦点
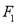 的直线l与椭圆C相交于
的直线l与椭圆C相交于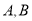 两点,若
两点,若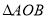 的面积为
的面积为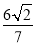 ,求圆心在原点O且与直线l相切的圆的方程。
,求圆心在原点O且与直线l相切的圆的方程。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校在2017年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示。
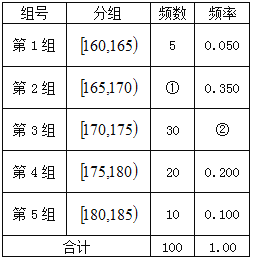
(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A教官进行面试,求:第4组至少有一名学生被考官A面试的概率?
相关试题

