【题目】设![]() 是定义在D上的函数,若对D中的任意两数
是定义在D上的函数,若对D中的任意两数![]() ),恒有
),恒有![]() ,则称
,则称![]() 为定义在D上的C函数.
为定义在D上的C函数.
(1)试判断函数![]() 是否为定义域上的C函数,并说明理由;
是否为定义域上的C函数,并说明理由;
(2)若函数![]() 是R上的奇函数,试证明
是R上的奇函数,试证明![]() 不是R上的C函数;
不是R上的C函数;
(3)设![]() 是定义在D上的函数,若对任何实数
是定义在D上的函数,若对任何实数![]() 以及D中的任意两数
以及D中的任意两数![]() ),恒有
),恒有![]() ,则称
,则称![]() 为定义在D上的π函数. 已知
为定义在D上的π函数. 已知![]() 是R上的π函数,m是给定的正整数,设
是R上的π函数,m是给定的正整数,设![]() ,且
,且![]() ,记
,记![]() . 对于满足条件的任意函数
. 对于满足条件的任意函数![]() ,试求
,试求![]() 的最大值.
的最大值.
参考答案:
【答案】(1)答案见解析;(2)证明见解析;(3) ![]() 的最大值为
的最大值为![]() .
.
【解析】试题分析:(1)证明![]() 是否成立,即可得出结论;(2)假设
是否成立,即可得出结论;(2)假设![]() 是R上的C函数,取
是R上的C函数,取![]() , 则有
, 则有![]() ,结合奇函数可得
,结合奇函数可得![]() ,是同理可得
,是同理可得![]() ,则推出矛盾;(3)对任意
,则推出矛盾;(3)对任意![]() ,取
,取![]() .由题意,
.由题意, ![]() =
= ![]() ≤
≤![]() =
=![]() ,则
,则![]() .
.
试题解析:(1) ![]() 是C函数,
是C函数,
证明如下:对任意实数![]() ),
),
有![]() =
=![]() =
=![]() .
.
即![]() ,
, ![]() 是C函数.
是C函数.
(2)假设![]() 是R上的C函数,取
是R上的C函数,取![]() ,
,
则有![]() .
.
![]() 是奇函数,所以
是奇函数,所以![]() ,所以
,所以![]() . (*)
. (*)
同理,取![]() ,可证
,可证![]() .与(*)式矛盾.
.与(*)式矛盾.
![]() 不是R上的C函数.
不是R上的C函数.
(3)对任意![]() ,取
,取![]() .
.
![]() 是R上的
是R上的![]() 函数,
函数, ![]() ,且
,且![]()
![]() =
= ![]() =
=![]() .
.
那么![]() =
= ![]() .
.
可证![]() 是
是![]() 函数,且使得
函数,且使得![]() 都成立,此时
都成立,此时![]() .
.
综上所述, ![]() 的最大值为
的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
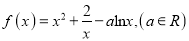 .
.(Ⅰ)若
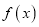 在
在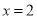 处取极值,求
处取极值,求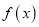 在点
在点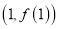 处的切线方程;
处的切线方程;(Ⅱ)当
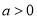 时,若
时,若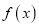 有唯一的零点
有唯一的零点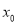 ,求证:
,求证: 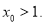
-
科目: 来源: 题型:
查看答案和解析>>【题目】【选修4-4:坐标系与参数方程】
极坐标系的极点为直角坐标系
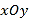 的原点,极轴为
的原点,极轴为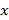 轴的正半轴,两神坐标系中的长度单位相同.已知曲线
轴的正半轴,两神坐标系中的长度单位相同.已知曲线 的极坐标方程为
的极坐标方程为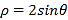 ,
, 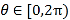 .
.(Ⅰ)求曲线
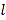 的直角坐标方程;
的直角坐标方程;(Ⅱ)在曲线
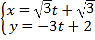 上求一点,使它到直线
上求一点,使它到直线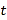 :
: 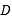 (
(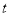 为参数)的距离最短,写出
为参数)的距离最短,写出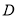 点的直角坐标.
点的直角坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】以A表示值域为R的函数组成的集合,B表示具有如下性质的函数
 组成的集合:对于函数
组成的集合:对于函数 ,存在一个正数M,使得函数
,存在一个正数M,使得函数 的值域包含于区间
的值域包含于区间 .例如,当
.例如,当 时,
时,  . 现有如下命题:
. 现有如下命题:①设函数
 的定义域为D,则“
的定义域为D,则“ ”的充要条件是“
”的充要条件是“ ”;
”;②若函数
 ,则
,则 有最大值和最小值;
有最大值和最小值;③若函数
 的定义域相同,且
的定义域相同,且 ,则
,则 ;
;④若函数
 有最大值,则
有最大值,则 .
.其中的真命题有___________. (写出所有真命题的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】以A表示值域为R的函数组成的集合,B表示具有如下性质的函数
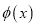 组成的集合:对于函数
组成的集合:对于函数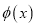 ,存在一个正数M,使得函数
,存在一个正数M,使得函数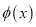 的值域包含于区间[-M,M]。例如,当
的值域包含于区间[-M,M]。例如,当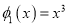 ,
, 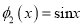 时,
时, 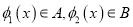 ,现有如下命题:
,现有如下命题:①设函数
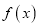 的定义域为D,则“
的定义域为D,则“ ”的充要条件是“
”的充要条件是“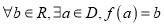 ”;
”;②若函数
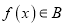 ,则
,则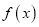 有最大值和最小值;
有最大值和最小值;③若函数
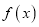 ,
, 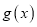 的定义域相同,且
的定义域相同,且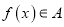 ,
, 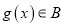 ,则
,则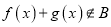
④若函数
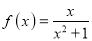 ,则
,则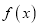 有最大值且
有最大值且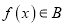 ,
,其中的真命题有_____________。(写出所有真命题的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分13分)已知数列
 的前
的前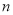 项和为
项和为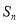 ,
, 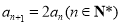 ,且
,且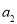 是
是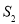 与
与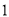 的等差中项.
的等差中项.(Ⅰ)求
 的通项公式;
的通项公式;(Ⅱ)若数列
 的前
的前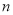 项和为
项和为 ,且对
,且对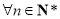 ,
,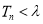 恒成立,求实数
恒成立,求实数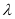 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分13分)已知函数
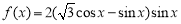 ,
,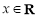 .
.(Ⅰ)求函数
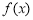 的最小正周期与单调增区间;
的最小正周期与单调增区间;(Ⅱ)求函数
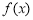 在
在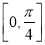 上的最大值与最小值.
上的最大值与最小值.
相关试题

