【题目】已知![]() ,
, ![]() ,曲线
,曲线![]() 上的任意一点
上的任意一点![]() 满足:
满足: ![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
, ![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,设
点,设![]() ,
, ![]() ,试问
,试问![]() 是否为定值?如果是定值,请求出这个定值,如果不是定值,请说明理由.
是否为定值?如果是定值,请求出这个定值,如果不是定值,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(Ⅰ)求出向量的坐标,利用条件化简,即可求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)分类讨论,利用![]() ,
, ![]() ,结合韦达定理,即可得出结论.
,结合韦达定理,即可得出结论.
试题解析:(1)设![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,
∵![]() ,∴
,∴![]() ,
,
化简得, ![]() 为所求点
为所求点![]() 的轨迹方程.
的轨迹方程.
(2)设![]() ,
, ![]() .
.
①当直线![]() 与
与![]() 轴不重合时,设直线
轴不重合时,设直线![]() 的方程为
的方程为![]() ,
,
则![]() ,从而
,从而![]() ,
, ![]() ,由
,由![]() 得
得
![]() ,
, ![]() ,
, ![]() ,
,
同理由![]() 得
得![]() ,
,
∴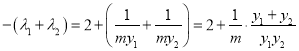 .①
.①
由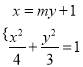 ,得
,得![]() .
.
∴![]() ,
, ![]() ,
,
代入①式得![]() ,∴
,∴![]() .
.
②当直线![]() 与
与![]() 轴重合时,
轴重合时, ![]() ,
, ![]() ,
, ![]() .
.
由![]() ,
, ![]() ,得
,得![]() ,
, ![]() ,∴
,∴![]() ,
,
综上, ![]() 为定值
为定值![]() .
.
点睛:定点、定值问题通常是通过设参数或取特殊值来确定“定点”是什么、“定值”是多少,或者将该问题涉及的几何式转化为代数式或三角问题,证明该式是恒定的. 定点、定值问题同证明问题类似,在求定点、定值之前已知该值的结果,因此求解时应设参数,运用推理,到最后必定参数统消,定点、定值显现.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知sinα+cosα=
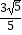 ,α∈(0,
,α∈(0,  ),sin(β﹣
),sin(β﹣  )=
)= 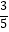 ,β∈(
,β∈(  ,
,  ).
).
(1)求sin2α和tan2α的值;
(2)求cos(α+2β)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ<
 )的部分图象如图所示.
)的部分图象如图所示. 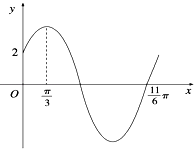
(1)求f(x)的解析式;
(2)将函数y=f(x)的图象上所有点的纵坐标不变,横坐标缩短为原来的 倍,再将所得函数图象向右平移
倍,再将所得函数图象向右平移  个单位,得到函数y=g(x)的图象,求g(x)的单调递增区间;
个单位,得到函数y=g(x)的图象,求g(x)的单调递增区间;
(3)当x∈[﹣ ,
, 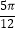 ]时,求函数y=f(x+
]时,求函数y=f(x+ 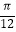 )﹣
)﹣ 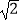 f(x+
f(x+  )的最值.
)的最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 =(cos
=(cos  x,sin
x,sin  x),
x),  =(cos
=(cos  x,﹣sin
x,﹣sin  x),且x∈[0,
x),且x∈[0,  ].求:
].求:
(1) 及
及  ;
;
(2)若f(x)= ﹣2λ
﹣2λ  的最小值是﹣
的最小值是﹣  ,求λ的值.
,求λ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两名同学在5次数学考试中的成绩统计如下面的茎叶图所示,若A,B两人的平均成绩分别是xA , xB , 观察茎叶图,下列结论正确的是( )
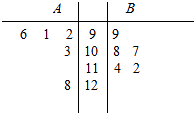
A.xA<xB , B比A成绩稳定
B.xA>xB , B比A成绩稳定
C.xA<xB , A比B成绩稳定
D.xA>xB , A比B成绩稳定 -
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图所示的程序框图,如果输入a=1,b=2,则输出的a的值为( )
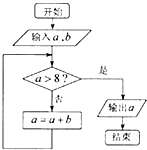
A.7
B.9
C.11
D.13 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个社会调查机构就某地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中再用分层抽样方法抽出80人作进一步调查,则在[1 500,2 000)(元)月收入段应抽出( )人.

A.15
B.16
C.17
D.18
相关试题

