搜索
【题目】已知函数
．
(I)求函数
的对称轴方程；
(II)将函数
的图象上各点的纵坐标保持不变，横坐标伸长为原来的2倍，然后再向左平移
个单位，得到函数
的图象．若
分别是△ABC三个内角A，B，C的对边，a=2，c=4，且
，求b的值．
参考答案：
【答案】（1）
（2）
【解析】试题分析:（1）先利用二倍角公式、配角公式将函数化为基本三角函数形式： 
，再根据正弦函数性质求对称轴，（2）先根据图像变换得到函数
的解析式，由
求出B
.再由余弦定理求b的值．
试题解析：解：（Ⅰ）函数
令
，解得
，
所以函数
的对称轴方程为
；
（Ⅱ）函数
的图象各点纵坐标不变，横坐标伸长为原来的2倍，得到函数
的图象，再向左平移
个单位，得到函数
的
图象，所以函数
.
又△
中， 
，所以
，又
，
所以
，则
.由余弦定理可知，
，
所以
-
科目： 来源： 题型：
查看答案和解析>>【题目】某品牌茶壶的原售价为80元/个，今有甲、乙两家茶具店销售这种茶壶，甲店用如下方法促销：如果只购买一个茶壶，其价格为78元/个；如果一次购买两个茶壶，其价格为76元/个；…，一次购买的茶壶数每增加一个，那么茶壶的价格减少2元/个，但茶壶的售价不得低于44元/个；乙店一律按原价的75%销售．现某茶社要购买这种茶壶x个，如果全部在甲店购买，则所需金额为y1元；如果全部在乙店购买，则所需金额为y2元．
（1）分别求出y1、y2与x之间的函数关系式；
（2）该茶社去哪家茶具店购买茶壶花费较少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】定义在R上的奇函数f（x），当x∈（﹣∞，0）时，f（x）=﹣x2+mx﹣1．
（1）当x∈（0，+∞）时，求f（x）的解析式；
（2）若方程f（x）=0有五个不相等的实数解，求实数m的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】某工程设备租赁公司为了调查A，B两种挖掘机的出租情况，现随机抽取了这两种挖掘机各100台，分别统计了每台挖掘机在一个星期内的出租天数，统计数据如下表：
(I)根据这个星期的统计数据，将频率视为概率，求该公司一台A型挖掘机，一台B型挖掘机一周内合计出租天数恰好为4天的概率；(II)如果A，B两种挖掘机每台每天出租获得的利润相同，该公司需要从A，B两种挖掘机中购买一台，请你根据所学的统计知识，给出建议应该购买哪一种类型，并说明你的理由．
-
科目： 来源： 题型：
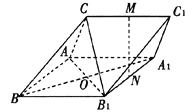
查看答案和解析>>【题目】如图，三棱柱ABC-A1B1Cl中，M，N分别为CC1，A1B1的中点．
(I)证明：直线MN／/平面CAB1；
(II)BA=BC=BB1，CA=CB1，CA⊥CB1，∠ABB1=60°，求平面AB1C和平面A1B1C1所成的角(锐角)的余弦值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知椭圆
的上、下焦点分别为
，上焦点
到直线 4x+3y+12=0的距离为3，椭圆C的离心率e=
．(I)若P是椭圆C上任意一点，求
的取值范围；(II)设过椭圆C的上顶点A的直线
与椭圆交于点B(B不在y轴上)，垂直于
的直线与
交于点M，与
轴交于点H，若
，且
，求直线
的方程．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
．(I)讨论函数
在
上的单调性；(II)设函数
存在两个极值点，并记作
，若
，求正数
的取值范围； (III)求证：当
=1时， 
（其中e为自然对数的底数）
相关试题
