【题目】已知函数![]() .
.
(I)讨论函数![]() 在
在![]() 上的单调性;
上的单调性;
(II)设函数![]() 存在两个极值点,并记作
存在两个极值点,并记作![]() ,若
,若![]() ,求正数
,求正数![]() 的取值范围;
的取值范围;
(III)求证:当![]() =1时,
=1时, ![]() (其中e为自然对数的底数)
(其中e为自然对数的底数)
参考答案:
【答案】(1)当![]() 时,函数
时,函数![]() 在
在![]() 上是增函数;当
上是增函数;当![]() 时,函数
时,函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.(2)正数
上是增函数.(2)正数![]() 的取值范围是
的取值范围是![]() .(3)见解析
.(3)见解析
【解析】试题分析:(1)先求函数导数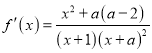 ,,再讨论导函数在定义区间上符号变化规律:当
,,再讨论导函数在定义区间上符号变化规律:当![]() 时,
时, ![]() ,即在
,即在![]() 上是增函数;当
上是增函数;当![]() 时,导函数有一个零点,符号先负后正,对应区间先减后增,(2)由题意易得要使函数
时,导函数有一个零点,符号先负后正,对应区间先减后增,(2)由题意易得要使函数![]() 存在两个极值点,必有
存在两个极值点,必有![]() ,且极值点必为
,且极值点必为![]() ,
, ![]() ,因此
,因此![]() ,即正数
,即正数![]() 的取值范围是
的取值范围是![]() .再化简条件
.再化简条件![]() ,得
,得![]() ,利用导数研究其单调性:为单调减,因此正数
,利用导数研究其单调性:为单调减,因此正数![]() 的取值范围是
的取值范围是![]() .(3)要证不等式
.(3)要证不等式![]() ,即证
,即证![]() ,利用导数易得函数
,利用导数易得函数![]() 最小值为1,而
最小值为1,而![]() ,得证.
,得证.
试题解析:(Ⅰ)  ,(
,( ![]() )
)
当![]() 时,
时, ![]() ,
, ![]()
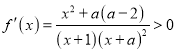 ,函数
,函数![]() 在
在![]() 上是增函数;
上是增函数;
当![]() 时,由
时,由![]() ,得
,得![]() ,解得
,解得![]() (负值舍去),
(负值舍去),![]() ,所以
,所以
当![]() 时,
时, ![]() ,从而
,从而![]() ,函数
,函数![]() 在
在![]() 上是减函数;
上是减函数;
当![]() 时,
时, ![]() ,从而
,从而![]() ,函数
,函数![]() 在
在![]() 上是增函数.
上是增函数.
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上是增函数;
上是增函数;
当![]() 时,函数
时,函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
(Ⅱ)由(Ⅰ)知,当![]() 时,
时, ![]() ,函数
,函数![]() 无极值点;
无极值点;
要使函数![]() 存在两个极值点,必有
存在两个极值点,必有![]() ,且极值点必为
,且极值点必为![]() ,
, ![]() ,又由函数定义域知,
,又由函数定义域知, ![]() ,则有
,则有![]() ,即
,即
![]() ,化为
,化为![]() ,所以
,所以![]() ,
,
所以,函数![]() 存在两个极值点时,正数
存在两个极值点时,正数![]() 的取值范围是
的取值范围是![]() .
.
由(![]() )式可知,
)式可知, ![]()
![]()
![]()
![]()
![]()
不等式![]() 化为
化为![]() ,
,
令![]() ,所以
,所以![]() ,
,
令![]() ,
, ![]() .
.
当![]() 时,
时, ![]() ,
, ![]() ,所以
,所以![]() ,不合题意;
,不合题意;
当![]() 时,
时, ![]() ,
, ![]() ,所以
,所以
![]() 在
在![]() 是减函数,所以
是减函数,所以![]() ,适合题意,即
,适合题意,即![]() .
.
综上,若![]() ,此时正数
,此时正数![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)当![]() 时,
时, ![]() ,
,
不等式![]() 可化为
可化为![]() ,所以
,所以
要证不等式![]() ,即证
,即证![]() ,即证
,即证![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 上,h'(x)<0,h(x)是减函数;
上,h'(x)<0,h(x)是减函数;
在![]() 上,h'(x)>0,h(x)是增函数.
上,h'(x)>0,h(x)是增函数.
所以![]() ,
,
设![]() ,则
,则![]() 是减函数,
是减函数,
所以![]() ,
,
所以![]() ,即
,即![]() ,
,
所以当![]() 时,不等式
时,不等式![]() 成立.
成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
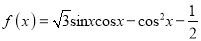 .
.(I)求函数
 的对称轴方程;
的对称轴方程;(II)将函数
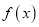 的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移
的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移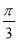 个单位,得到函数
个单位,得到函数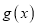 的图象.若
的图象.若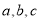 分别是△ABC三个内角A,B,C的对边,a=2,c=4,且
分别是△ABC三个内角A,B,C的对边,a=2,c=4,且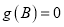 ,求b的值.
,求b的值. -
科目: 来源: 题型:
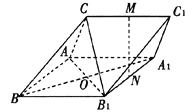
查看答案和解析>>【题目】如图,三棱柱ABC-A1B1Cl中,M,N分别为CC1,A1B1的中点.
(I)证明:直线MN//平面CAB1;
(II)BA=BC=BB1,CA=CB1,CA⊥CB1,∠ABB1=60°,求平面AB1C和平面A1B1C1所成的角(锐角)的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的上、下焦点分别为
的上、下焦点分别为 ,上焦点
,上焦点 到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=
到直线 4x+3y+12=0的距离为3,椭圆C的离心率e= .
.(I)若P是椭圆C上任意一点,求
 的取值范围;
的取值范围;(II)设过椭圆C的上顶点A的直线
 与椭圆交于点B(B不在y轴上),垂直于
与椭圆交于点B(B不在y轴上),垂直于 的直线与
的直线与 交于点M,与
交于点M,与 轴交于点H,若
轴交于点H,若 ,且
,且 ,求直线
,求直线 的方程.
的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:x∈R,kx2+1≤0,命题q:x∈R,x2+2kx+1>0.
(1)当k=3时,写出命题p的否定,并判断真假;
(2)当p∨q为假命题时,求实数k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn.求满足不等式
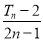 >2010的n的最小值.
>2010的n的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
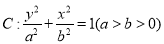 的上、下焦点分别为
的上、下焦点分别为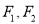 ,上焦点
,上焦点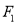 到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=
到直线 4x+3y+12=0的距离为3,椭圆C的离心率e= .
.(I)求椭圆C的标准方程;
(II)设过椭圆C的上顶点A的直线
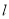 与椭圆交于点B(B不在y轴上),垂直于
与椭圆交于点B(B不在y轴上),垂直于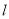 的直线与
的直线与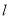 交于点M,与
交于点M,与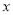 轴交于点H,若
轴交于点H,若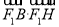 =0,且
=0,且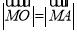 ,求直线
,求直线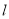 的方程.
的方程.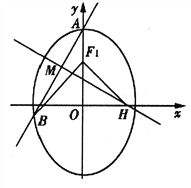
相关试题

