【题目】已知R是实数集,集合A={x|( ![]() )2x+1≤
)2x+1≤ ![]() },B={x|log4(3﹣x)<0.5},则(RA)∩B=( )
},B={x|log4(3﹣x)<0.5},则(RA)∩B=( )
A.(1,2)
B.(1,2)
C.(1,3)
D.(1,1.5)
参考答案:
【答案】D
【解析】解:集合A={x|( ![]() )2x+1≤
)2x+1≤ ![]() }={x|2x+1≥4}={x|x≥
}={x|2x+1≥4}={x|x≥ ![]() },
},
B={x|log4(3﹣x)<0.5}={x|0<3﹣x<2}={x|1<x<3},
∴RA={x|x< ![]() },
},
∴(RA)∩B={x|1<x< ![]() }=(1,1.5).
}=(1,1.5).
故选:D.
【考点精析】根据题目的已知条件,利用交、并、补集的混合运算的相关知识可以得到问题的答案,需要掌握求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】古希腊杰出的数学家丢番图的墓碑上有这样一首诗:
这是一座古墓,里面安葬着丢番图.
请你告诉我,丢番图的寿数几何?
他的童年占去了一生的六分之一,
接着十二分之一是少年时期,
又过了七分之一的时光,他找到了自己的终身伴侣.
五年之后,婚姻之神赐给他一个儿子,
可是儿子不济,只活到父亲寿数的一半,就匆匆离去.
这对父亲是一个沉重的打击,
整整四年,为失去爱子而悲伤,
终于告别了数学,离开了人世.
试用循环结构,写出算法分析和算法程序.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2018海南高三阶段性测试(二模)】如图,在直三棱柱
 中,
中,  ,
,  ,点
,点 为
为 的中点,点
的中点,点 为
为 上一动点.
上一动点.
(I)是否存在一点
 ,使得线段
,使得线段 平面
平面 ?若存在,指出点
?若存在,指出点 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.(II)若点
 为
为 的中点且
的中点且 ,求三棱锥
,求三棱锥 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知由甲、乙两位男生和丙、丁两位女生组成的四人冲关小组,参加由安徽卫视推出的大型户外竞技类活动《男生女生向前冲》.活动共有四关,若四关都闯过,则闯关成功,否则落水失败.设男生闯过一至四关的概率依次是
 ,
, 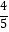 ,
,  ,
,  ,女生闯过一至四关的概率依次是
,女生闯过一至四关的概率依次是 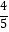 ,
,  ,
,  ,
,  .
.
(Ⅰ)求男生甲闯关失败的概率;
(Ⅱ)设X表示四人冲关小组闯关成功的人数,求随机变量X的分布列和期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知边长为
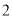 的正方形
的正方形 与菱形
与菱形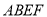 所在平面互相垂直,
所在平面互相垂直, 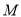 为
为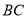 中点.
中点.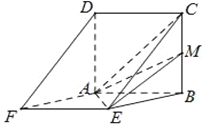
(1)求证:
 平面
平面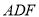 ;
;(2)若
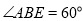 ,求四面体
,求四面体 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 的底面是直角梯形,
的底面是直角梯形,  ,
,  ,
, ,点
,点 在线段
在线段 上,且
上,且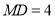 ,
,  ,
,  平面
平面 .
.(1)求证:平面
 平面
平面 ;
;(2)当四棱锥
 的体积最大时,求四棱锥
的体积最大时,求四棱锥 的表面积.
的表面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,
中,  ,
,  与
与 交于
交于 点,现将
点,现将 沿
沿 折起得到三棱锥
折起得到三棱锥 ,
,  ,
, 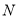 分别是
分别是 ,
,  的中点.
的中点.
(1)求证:
 ;
;(2)若三棱锥
 的最大体积为
的最大体积为 ,当三棱锥
,当三棱锥 的体积为
的体积为 ,且
,且 为锐角时,求三棱锥
为锐角时,求三棱锥 的体积.
的体积.
相关试题

