【题目】已知函数y=﹣x2+ax﹣ ![]() 在区间[0,1]上的最大值是2,求实数a的值.
在区间[0,1]上的最大值是2,求实数a的值.
参考答案:
【答案】解:∵y=f(x)=﹣ ![]() +
+ ![]() (a2﹣a+2),对称轴为x=
(a2﹣a+2),对称轴为x= ![]() ,
,
(I)当0≤ ![]() ≤1时,即0≤a≤2时,f(x)max=
≤1时,即0≤a≤2时,f(x)max= ![]() (a2﹣a+2),
(a2﹣a+2),
由 ![]() (a2﹣a+2)=2得a=﹣2或a=3与0≤a≤2矛盾,不和要求
(a2﹣a+2)=2得a=﹣2或a=3与0≤a≤2矛盾,不和要求
(II)当 ![]() <0,即a<0时,f(x)在[0,1]上单调递减,f(x)max=f(0),由f(0)=2
<0,即a<0时,f(x)在[0,1]上单调递减,f(x)max=f(0),由f(0)=2
得﹣ ![]() +
+ ![]() =2,解得a=﹣6
=2,解得a=﹣6
(III)当 ![]() >1,即a>2时,f(x)在[0,1]上单调递增,f(x)max=f(1),
>1,即a>2时,f(x)在[0,1]上单调递增,f(x)max=f(1),
由f(1)=2得:﹣1+a﹣ ![]() +
+ ![]() =2,解得a=
=2,解得a= ![]()
综上所述,a=﹣6或a= ![]()
【解析】先求对称轴,比较对称轴和区间的关系,利用开口向下的二次函数离对称轴越近函数值越大来解题.
【考点精析】根据题目的已知条件,利用二次函数在闭区间上的最值的相关知识可以得到问题的答案,需要掌握当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
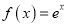 ,
, 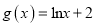 .
.(1)若直线
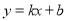 是曲线
是曲线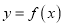 与曲线
与曲线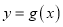 的公切线,求
的公切线,求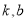 ;
;(2)设
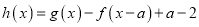 ,若
,若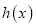 有两个零点,求
有两个零点,求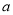 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在底面半径为6的圆柱内,有两个半径也为6的球面,两球的球心距为13,若作一个平面与两个球都相切,且与圆柱面相交成一椭圆,则椭圆的长轴长为。
-
科目: 来源: 题型:
查看答案和解析>>【题目】一大学生自主创业,拟生产并销售某电子产品
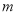 万件(生产量与销售量相等),为扩大影响进行促销,促销费用
万件(生产量与销售量相等),为扩大影响进行促销,促销费用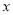 (万元)满足
(万元)满足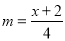 (其中
(其中 为正常数).已知生产该产品还需投入成本
为正常数).已知生产该产品还需投入成本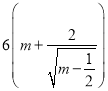 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为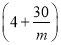 元/件.
元/件.(1)将该产品的利润
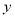 万元表示为促销费用
万元表示为促销费用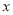 万元的函数;
万元的函数;(2)促销费用投入多少万元时,此大学生所获利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年10月28日,经历了近半个世纪风雨的南京长江大桥真“累”了,终于停下来喘口气了,之前大桥在改善我们城市的交通状况方面功不可没.据相关数据统计,一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到280辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过30辆/千米时,车流速度为50千米/小时.研究表明,当30≤x≤280时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤280时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时) f(x)=xv(x)可以达到最大,并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4—5:不等式选讲]
已知
 .
.(1)若
 的解集为
的解集为 ,求
,求 的值;
的值;(2)若
 不等式
不等式 恒成立,求实数
恒成立,求实数 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 +m为奇函数,m为常数.
+m为奇函数,m为常数.
(1)求实数m的值;
(2)判断并证明f(x)的单调性;
(3)若关于x的不等式f(f(x))+f(ma)<0有解,求实数a的取值范围.
相关试题

