【题目】一大学生自主创业,拟生产并销售某电子产品![]() 万件(生产量与销售量相等),为扩大影响进行促销,促销费用
万件(生产量与销售量相等),为扩大影响进行促销,促销费用![]() (万元)满足
(万元)满足![]() (其中
(其中![]() 为正常数).已知生产该产品还需投入成本
为正常数).已知生产该产品还需投入成本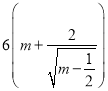 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 元/件.
元/件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,此大学生所获利润最大?
参考答案:
【答案】(1)![]() ;(2)当
;(2)当![]() 时,投入4万元时,利润最大;当
时,投入4万元时,利润最大;当![]() 时,投入
时,投入![]() 万元时,利润最大.
万元时,利润最大.
【解析】试题分析: (1)利用销售收入与成本的差,结合![]() 即可该产品的利润
即可该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;(2)由(1)可得
万元的函数;(2)由(1)可得![]()
,讨论![]() 、
、![]() ,分别利用导数研究函数的单调性,从而可得结果.
,分别利用导数研究函数的单调性,从而可得结果.
试题解析:(1)由题意知, 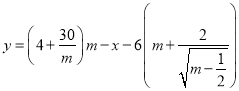 将
将![]() 代入化简得:
代入化简得:
![]() .
.
(2)![]()
令![]()
故![]() 在
在![]() 单调递减,
单调递减, ![]() 单调递增,
单调递增, ![]()
所以![]() 万元,当且仅当
万元,当且仅当![]() 取得.
取得.
当![]() 时,促销费用投入4万元时,该大学生获得的利润最大,最大为
时,促销费用投入4万元时,该大学生获得的利润最大,最大为![]() 万元;
万元;
当![]() 时,函数在
时,函数在![]() 上单调递增,
上单调递增,
∴![]() 时,函数有最大值.即促销费用投入
时,函数有最大值.即促销费用投入![]() 万元时,该大学生获得的利润最大,最大为
万元时,该大学生获得的利润最大,最大为![]() 万元.
万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4―4:坐标系与参数方程]
在平面直角坐标系中,以坐标原点
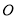 为极点,
为极点,  轴的正半轴为极轴建立极坐标系.已知直线
轴的正半轴为极轴建立极坐标系.已知直线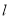 的参数方程为
的参数方程为 ;曲线
;曲线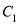 的极坐标方程为
的极坐标方程为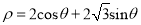 ;曲线
;曲线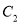 的参数方程为
的参数方程为 (
(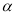 为参数).
为参数).(1)求直线
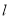 的直角坐标方程、曲线
的直角坐标方程、曲线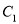 的直角坐标方程和曲线
的直角坐标方程和曲线 的普通方程;
的普通方程;(2)若直线
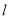 与曲线
与曲线 曲线
曲线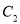 在第一象限的交点分别为
在第一象限的交点分别为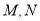 ,求
,求 之间的距离.
之间的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
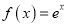 ,
, 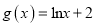 .
.(1)若直线
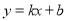 是曲线
是曲线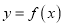 与曲线
与曲线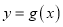 的公切线,求
的公切线,求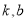 ;
;(2)设
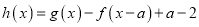 ,若
,若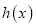 有两个零点,求
有两个零点,求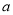 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在底面半径为6的圆柱内,有两个半径也为6的球面,两球的球心距为13,若作一个平面与两个球都相切,且与圆柱面相交成一椭圆,则椭圆的长轴长为。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=﹣x2+ax﹣
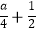 在区间[0,1]上的最大值是2,求实数a的值.
在区间[0,1]上的最大值是2,求实数a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年10月28日,经历了近半个世纪风雨的南京长江大桥真“累”了,终于停下来喘口气了,之前大桥在改善我们城市的交通状况方面功不可没.据相关数据统计,一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到280辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过30辆/千米时,车流速度为50千米/小时.研究表明,当30≤x≤280时,车流速度v是车流密度x的一次函数.
(1)当0≤x≤280时,求函数v(x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时) f(x)=xv(x)可以达到最大,并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4—5:不等式选讲]
已知
 .
.(1)若
 的解集为
的解集为 ,求
,求 的值;
的值;(2)若
 不等式
不等式 恒成立,求实数
恒成立,求实数 的范围.
的范围.
相关试题

