【题目】求下列函数的定义域和值域:
(1)y=3 ![]()
(2)y= ![]()
(3)y=log2 ![]() .
.
参考答案:
【答案】
(1)解:y=3 ![]()
定义域满足:2x+1≠0,解得:x ![]() ,
,
故得定义域为{x| ![]() }.
}.
∵ ![]() ,且3
,且3 ![]() >0,
>0,
∴3 ![]() ≠1
≠1
故得值域为{y|y>0且y≠1}
(2)解:y= ![]()
定义域满足: ![]() ,解得:x≥0,
,解得:x≥0,
∵ ![]() 且
且 ![]() ,
,
故得: ![]() ,
,
∴0≤ ![]() <1,
<1,
故得值域为{y|1>y≥0}
(3)解:y=log2 ![]() .
.
定义域满足: ![]() ,即1﹣3x>0,解得:x<0,
,即1﹣3x>0,解得:x<0,
故得定义域为{x|x<0}.
∵3x>0,且1﹣3x>0,即1﹣3x<1,
故: ![]() ,
,
∴log2 ![]() >0
>0
故得定义域为{y|y>0}
【解析】根据函数解析式有意义列出x意义的不等式和根据定义域来求解值域.
【考点精析】掌握函数的值域是解答本题的根本,需要知道求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
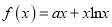 图象在点
图象在点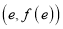 (e为自然对数的底数)处的切线斜率为3.
(e为自然对数的底数)处的切线斜率为3.(1)求实数
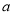 的值;
的值;(2)若
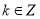 ,且
,且 对任意
对任意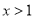 恒成立,求
恒成立,求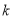 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1) =3;
=3;
(2)log4(3x﹣1)=log4(x﹣1)+log4(3+x). -
科目: 来源: 题型:
查看答案和解析>>【题目】比较下列各题中两个数的大小:
(1)log60.8,log69.1;
(2)log0.17,log0.19;
(3)log0.15,log2.35
(4)loga4,loga6(a>0,且a≠1) -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数f(x)的图象与x轴交于(﹣2,0),(4,0)两点,且顶点为(1,﹣
 ).
).
(1)求f(x)的函数解析式;
(2)指出图象的开口方向、对称轴和顶点坐标;
(3)分析函数的单调性,求函数的最大值或最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,且2csinBcosA﹣bsinC=0.
(1)求角A;
(2)若△ABC的面积为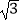 ,b+c=5,求a.
,b+c=5,求a. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知全集U=R,集合A={x|x<﹣4,或x>1},B={x|﹣3≤x﹣1≤2},
(1)求A∩B、(UA)∪(UB);
(2)若集合M={x|2k﹣1≤x≤2k+1}是集合A的子集,求实数k的取值范围.
相关试题

