【题目】已知抛物线![]() :
: ![]() 的焦点
的焦点![]() 也是椭圆
也是椭圆![]() :
: ![]() (
(![]() )的一个焦点,
)的一个焦点, ![]() 与
与![]() 的公共弦长为
的公共弦长为![]() .
.
(Ⅰ)求![]() 的方程
的方程
(Ⅱ)过点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() ,
, ![]() 两点,与
两点,与![]() 相交于
相交于![]() ,
, ![]() 两点,且
两点,且![]() ,
, ![]() 同向.若
同向.若![]() 求直线
求直线![]() 的斜率;
的斜率;
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)由抛物线与椭圆共焦点可得![]() ,再由公共弦长可得公共点坐标
,再由公共弦长可得公共点坐标![]() 代入与前式联立可得
代入与前式联立可得![]() 的值;(Ⅱ)设
的值;(Ⅱ)设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]()
与双曲线联立,利用韦达定理,将![]() 转化为关于
转化为关于![]() 的方程,解可得直线的斜率. 试题解析:解:(1)由抛物线
的方程,解可得直线的斜率. 试题解析:解:(1)由抛物线![]() :
: ![]() 的焦点
的焦点![]() ,所以
,所以![]() ,又由
,又由![]() 与
与![]() 的公共弦长为
的公共弦长为![]() ,得公共点坐标
,得公共点坐标![]() ,所以
,所以![]() ,解得
,解得![]() ,
, ![]() 得
得![]() :
: ![]()
(2)设![]() ,
, ![]() ,
, ![]() ,
, ![]()
由![]() ,得
,得![]() ,所以
,所以![]() ①
①
设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]()
由![]() 得
得![]() ,
, ![]() ,
, ![]() ②
②
由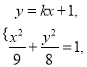 得
得![]() ,
, ![]() ,
, ![]() ③
③
将②③代入①,解得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面体的高的最小值为( )
A.
B.2+
C.4+
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个袋子,其中甲袋中装有编号分别为1、2、3、4的4个完全相同的球,乙袋中装有编号分别为2、4、6的3个完全相同的球.
(Ⅰ)从甲、乙袋子中各取一个球,求两球编号之和小于8的概率;
(Ⅱ)从甲袋中取2个球,从乙袋中取一个球,求所取出的3个球中含有编号为2的球的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某家具厂有方木料
 ,五合板
,五合板 ,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料
,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料 、五合板
、五合板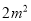 ;生产每个书橱需要方木枓
;生产每个书橱需要方木枓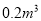 、五合板
、五合板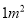 .出售一张书桌可获利润
.出售一张书桌可获利润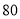 元,出售一个书橱可获利润
元,出售一个书橱可获利润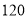 元,怎样安排生产可使所得利润最大?最大利润为多少?
元,怎样安排生产可使所得利润最大?最大利润为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】设有关x的一元二次方程9x2+6ax﹣b2+4=0.
(1)若a是从1,2,3这三个数中任取的一个数,b是从0,1,2这三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]中任取的一个数,b是从区间[0,2]中任取的一个数,求上述方程有实根的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,点M是平面A1B1C1D1内一点,且BM∥平面ACD1 , 则tan∠DMD1的最大值为( )

A.
B.1
C.2
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在边长为3的正三角形中,
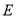 ,
, 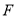 ,
, 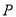 分别为
分别为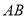 ,
, 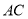 ,
, 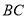 上的点,且满足
上的点,且满足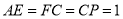 .将
.将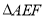 沿
沿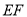 折起到
折起到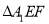 的位置,使平面
的位置,使平面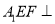 平面
平面 ,连结
,连结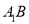 ,
,  ,
, 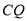 .(如图2)
.(如图2)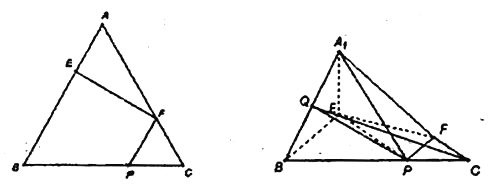
(Ⅰ)若
 为
为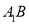 中点,求证:
中点,求证: 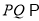 平面
平面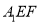 ;
;(Ⅱ)求证:
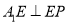 ;
;(Ⅲ)求
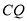 与平面
与平面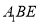 所成角的正切.
所成角的正切.
相关试题

