【题目】将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面体的高的最小值为( )
A.![]()
B.2+ ![]()
C.4+ ![]()
D.![]()
参考答案:
【答案】C
【解析】解:由题意知,底面放三个钢球,上再落一个钢球时体积最小. 于是把钢球的球心连接,则又可得到一个棱长为2的小正四面体,则不难求出这个小正四面体的高为 ![]() ,
,
且由正四面体的性质可知:正四面体的中心到底面的距离是高的 ![]() ,且小正四面体的中心和正四面体容器的中心应该是重合的,
,且小正四面体的中心和正四面体容器的中心应该是重合的,
∴小正四面体的中心到底面的距离是 ![]() ×
× ![]() =
= ![]() ,正四面体的中心到底面的距离是
,正四面体的中心到底面的距离是 ![]() +1 (1即小钢球的半径),
+1 (1即小钢球的半径),
所以可知正四棱锥的高的最小值为 ( ![]() +1)×4=4+
+1)×4=4+ ![]() ,
,
故选 C.
【考点精析】掌握棱锥的结构特征是解答本题的根本,需要知道侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在四面体ABCD中,E,F分别是AC,BD的中点,若AB=2,CD=4,EF⊥AB,则EF与CD所成的角的度数为( )
A.90°
B.45°
C.60°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】一盒中装有各色球12只,其中5个红球,4个黑球,2个白球,1个绿球;从中随机取出1球.求:
(1)取出的1球是红球或黑球的概率;
(2)取出的1球是红球或黑球或白球的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的图象与函数
的图象与函数 的图象关于
的图象关于 轴对称,若函数
轴对称,若函数 与函数
与函数 在区间
在区间 上同时单调递增或同时单调递减,则实数
上同时单调递增或同时单调递减,则实数 的取值范围是( )
的取值范围是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个袋子,其中甲袋中装有编号分别为1、2、3、4的4个完全相同的球,乙袋中装有编号分别为2、4、6的3个完全相同的球.
(Ⅰ)从甲、乙袋子中各取一个球,求两球编号之和小于8的概率;
(Ⅱ)从甲袋中取2个球,从乙袋中取一个球,求所取出的3个球中含有编号为2的球的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某家具厂有方木料
 ,五合板
,五合板 ,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料
,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料 、五合板
、五合板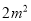 ;生产每个书橱需要方木枓
;生产每个书橱需要方木枓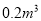 、五合板
、五合板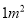 .出售一张书桌可获利润
.出售一张书桌可获利润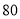 元,出售一个书橱可获利润
元,出售一个书橱可获利润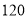 元,怎样安排生产可使所得利润最大?最大利润为多少?
元,怎样安排生产可使所得利润最大?最大利润为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 :
: 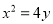 的焦点
的焦点 也是椭圆
也是椭圆 :
:  (
( )的一个焦点,
)的一个焦点,  与
与 的公共弦长为
的公共弦长为 .
.(Ⅰ)求
 的方程
的方程(Ⅱ)过点
 的直线
的直线 与
与 相交于
相交于 ,
,  两点,与
两点,与 相交于
相交于 ,
,  两点,且
两点,且 ,
,  同向.若
同向.若 求直线
求直线 的斜率;
的斜率;
相关试题

