【题目】设有关x的一元二次方程9x2+6ax﹣b2+4=0.
(1)若a是从1,2,3这三个数中任取的一个数,b是从0,1,2这三个数中任取的一个数,求上述方程有实根的概率;
(2)若a是从区间[0,3]中任取的一个数,b是从区间[0,2]中任取的一个数,求上述方程有实根的概率.
参考答案:
【答案】解:(1)由题意,知基本事件共有9个,可用有序实数对表示为(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2),
其中第一个表示a的取值,第二个表示b的取值
由方程9x2+6ax﹣b2+4=0的△=36a2﹣36(﹣b2+4)≥0a2+b2≥4
∴方程9x2+6ax﹣b2+4=0有实根包含7个基本事件,即(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2).
∴此时方程9x2+6ax﹣b2+4=0有实根的概率为![]()
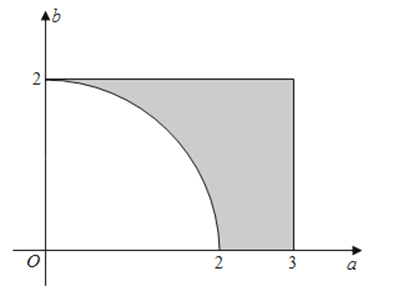
(2)a,b的取值所构成的区域如图所示,其中0≤a≤3,0≤b≤2
∴构成“方程9x2+6ax﹣b2+4=0有实根”这一事件的区域为{(a,b)|a2+b2≥4,0≤a≤3,0≤b≤2}(图中阴影部分).
∴此时所求概率为![]()
【解析】(1)利用有序实数对表示基本事件,由古典概型公式解答;
(2)表示a,b满足的区域,求出面积,利用几何概型解答.
【考点精析】通过灵活运用几何概型,掌握几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个袋子,其中甲袋中装有编号分别为1、2、3、4的4个完全相同的球,乙袋中装有编号分别为2、4、6的3个完全相同的球.
(Ⅰ)从甲、乙袋子中各取一个球,求两球编号之和小于8的概率;
(Ⅱ)从甲袋中取2个球,从乙袋中取一个球,求所取出的3个球中含有编号为2的球的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某家具厂有方木料
 ,五合板
,五合板 ,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料
,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料 、五合板
、五合板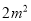 ;生产每个书橱需要方木枓
;生产每个书橱需要方木枓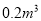 、五合板
、五合板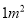 .出售一张书桌可获利润
.出售一张书桌可获利润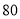 元,出售一个书橱可获利润
元,出售一个书橱可获利润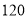 元,怎样安排生产可使所得利润最大?最大利润为多少?
元,怎样安排生产可使所得利润最大?最大利润为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 :
: 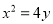 的焦点
的焦点 也是椭圆
也是椭圆 :
:  (
( )的一个焦点,
)的一个焦点,  与
与 的公共弦长为
的公共弦长为 .
.(Ⅰ)求
 的方程
的方程(Ⅱ)过点
 的直线
的直线 与
与 相交于
相交于 ,
,  两点,与
两点,与 相交于
相交于 ,
,  两点,且
两点,且 ,
,  同向.若
同向.若 求直线
求直线 的斜率;
的斜率; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,点M是平面A1B1C1D1内一点,且BM∥平面ACD1 , 则tan∠DMD1的最大值为( )

A.
B.1
C.2
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在边长为3的正三角形中,
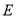 ,
, 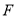 ,
, 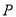 分别为
分别为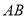 ,
, 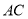 ,
, 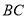 上的点,且满足
上的点,且满足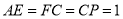 .将
.将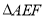 沿
沿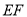 折起到
折起到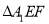 的位置,使平面
的位置,使平面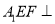 平面
平面 ,连结
,连结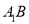 ,
,  ,
, 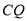 .(如图2)
.(如图2)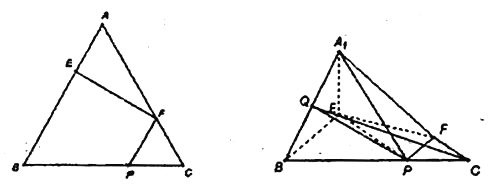
(Ⅰ)若
 为
为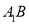 中点,求证:
中点,求证: 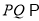 平面
平面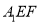 ;
;(Ⅱ)求证:
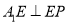 ;
;(Ⅲ)求
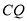 与平面
与平面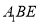 所成角的正切.
所成角的正切. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知单调递增的等比数列
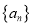 满足
满足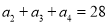 ,且
,且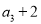 是
是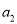 ,
, 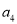 的等差中项.
的等差中项.(Ⅰ)求数列
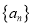 的通项公式;
的通项公式;(Ⅱ)若数列
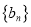 满足
满足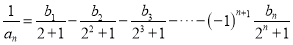 ,求数列
,求数列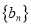 的通项公式;
的通项公式;(Ⅲ)在(Ⅱ)的条件下,设
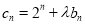 ,问是否存在实数
,问是否存在实数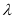 使得数列
使得数列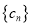 (
(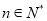 )是单调递增数列?若存在,求出
)是单调递增数列?若存在,求出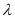 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
相关试题

