【题目】已知函数 ![]() (
( ![]() 为实常数).
为实常数).
(1)若 ![]() ,
, ![]() ,求
,求 ![]() 的单调区间;
的单调区间;
(2)若 ![]() ,且
,且 ![]() ,求函数
,求函数 ![]() 在
在 ![]() 上的最小值及相应的
上的最小值及相应的 ![]() 值;
值;
(3)设 ![]() ,若存在
,若存在 ![]() ,使得
,使得 ![]() 成立,求实数
成立,求实数 ![]() 的取值范围.
的取值范围.
参考答案:
【答案】
(1)解: ![]() 时,
时, ![]() ,
,
定义域为 ![]() ,
, ![]()
在 ![]() 上,
上, ![]() ,当
,当 ![]() 时,
时, ![]() ;当
;当 ![]() 时,
时, ![]()
所以,函数 ![]() 的单调增区间为
的单调增区间为 ![]() ;单调减区间为
;单调减区间为 ![]()
(2)解:因为 ![]() ,所以
,所以 ![]() ,
, ![]() ,
, ![]() ,
, ![]()
(Ⅰ)若 ![]() ,
, ![]() 在
在 ![]() 上非负(仅当
上非负(仅当 ![]() 时,
时, ![]() ),
),
故函数 ![]() 在
在 ![]() 上是增函数,此时
上是增函数,此时 ![]()
(Ⅱ)若 ![]() ,
, ![]() ,
, ![]()
当 ![]() 时,
时, ![]() ,
, ![]()
当 ![]() 时,
时, ![]() ,此时
,此时 ![]() 是减函数;
是减函数;
当 ![]() 时,
时, ![]() ,此时
,此时 ![]() 是增函数,
是增函数,
故 ![]()
(3)解: ![]() ,
, ![]()
不等式 ![]() ,即
,即 ![]() 可化为
可化为 ![]() .
.
因为 ![]() , 所以
, 所以 ![]() 且等号不能同时取,
且等号不能同时取,
所以 ![]() ,即
,即 ![]() ,因而
,因而 ![]() (
( ![]() )
)
令 ![]() (
( ![]() ),又
),又 ![]() ,
,
当 ![]() 时,
时, ![]() ,
, ![]() ,
,
从而 ![]() (仅当
(仅当 ![]() 时取等号),所以
时取等号),所以 ![]() 在
在 ![]() 上为增函数,
上为增函数,
故 ![]() 的最小值为
的最小值为 ![]() ,所以实数
,所以实数 ![]() 的取值范围是
的取值范围是 ![]()
【解析】(1)首先求出函数的导函数,解关于导函数的不等式求出函数的单调区间即可。(2)求出函数的导函数通过讨论a的取值范围求出函数的单调区间进而求出函数的最小值即可。(3)根据题意把问题转化为![]() ( x ∈ [ 1 , e ] )构造函数g(x),利用该函数的单调性即可求出a 的取值范围。
( x ∈ [ 1 , e ] )构造函数g(x),利用该函数的单调性即可求出a 的取值范围。
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
 的右焦点为
的右焦点为 ,右顶点为
,右顶点为 ,已知
,已知 ,其中
,其中 为原点,
为原点, 为椭圆的离心率.
为椭圆的离心率.(1)求椭圆的方程;
(2)设过点
 的直线
的直线 与椭圆交于点
与椭圆交于点 (
( 不在
不在 轴上),垂直于
轴上),垂直于 的直线与
的直线与 交于点
交于点 ,与
,与 轴交于点
轴交于点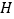 ,若
,若 ,且
,且 ,求直线的
,求直线的 斜率的取值范围.
斜率的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(选修4﹣4:坐标系与参数方程):
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,已知射线θ= 与曲线
与曲线  (t为参数)相交于A,B来两点,则线段AB的中点的直角坐标为 .
(t为参数)相交于A,B来两点,则线段AB的中点的直角坐标为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,直线C的参数方程为
 为参数),曲线P在以该直角坐标系的原点O的为极点,x轴的正半轴为极轴的极坐标系下的方程为ρ2﹣4ρcosθ+3=0.
为参数),曲线P在以该直角坐标系的原点O的为极点,x轴的正半轴为极轴的极坐标系下的方程为ρ2﹣4ρcosθ+3=0.
(1)求直线C的普通方程和曲线P的直角坐标方程;
(2)设直线C和曲线P的交点为A、B,求|AB|. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,直线l的参数方程是
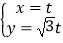 (t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为ρ2cos2θ+ρ2sin2θ﹣2ρsinθ﹣3=0.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为ρ2cos2θ+ρ2sin2θ﹣2ρsinθ﹣3=0.
(1)求直线l的极坐标方程;
(2)若直线l与曲线C相交于A、B两点,求|AB|. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,直线l的参数方程为
 (t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位.且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=6sinθ.
(t为参数)在极坐标系(与直角坐标系xOy取相同的长度单位.且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=6sinθ.
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A,B.若点P的坐标为(1,2),求|PA|+|PB|的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,以原点为极点,
 轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线
轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线  的极坐标方程为
的极坐标方程为  ,直线
,直线  的参数方程为
的参数方程为 (
(  为参数,
为参数,  为直线的倾斜角).
为直线的倾斜角).
(1)写出直线 的普通方程和曲线
的普通方程和曲线  的直角坐标方程;
的直角坐标方程;
(2)若直线 与曲线
与曲线  有唯一的公共点,求角
有唯一的公共点,求角  的大小.
的大小.
相关试题

