【题目】设数列![]() 满足
满足![]() ,
,![]() .
.
(1)求![]() ;
;
(2)先猜想出![]() 的一个通项公式,再用数学归纳法证明你的猜想.
的一个通项公式,再用数学归纳法证明你的猜想.
参考答案:
【答案】(1)5,7,9;(2)猜想![]() ;证明祥见解析.
;证明祥见解析.
【解析】
试题分析:(1)由已知等式:![]() 令n=1,再将
令n=1,再将![]() 代入即可求得
代入即可求得![]() 的值;再令n=2并将
的值;再令n=2并将![]() 的值就可求得
的值就可求得![]() 的值;最后再令n=2并将
的值;最后再令n=2并将![]() 的值就可求得
的值就可求得![]() 的值;(2)由已知及(1)的结果,可猜想出
的值;(2)由已知及(1)的结果,可猜想出![]() 的一个通项公式;用数学归纳法证明时应注意格式:①验证
的一个通项公式;用数学归纳法证明时应注意格式:①验证![]() 时猜想正确;②作归纳假设:假设当
时猜想正确;②作归纳假设:假设当![]() 时,猜想成立,在此基础上来证明
时,猜想成立,在此基础上来证明![]() 时猜想也成立,注意在此证明过程中要充分利用已知条件找出
时猜想也成立,注意在此证明过程中要充分利用已知条件找出![]() 之间的关系,并一定要用到假设当
之间的关系,并一定要用到假设当![]() 时的结论;最后一定要下结论.
时的结论;最后一定要下结论.
试题解析: (1)由条件![]() ,依次得
,依次得![]() ,
,
![]() ,
,![]() , 6分
, 6分
(2)由(1),猜想![]() . 7分
. 7分
下用数学归纳法证明之:
①当![]() 时,
时,![]() ,猜想成立; 8分
,猜想成立; 8分
②假设当![]() 时,猜想成立,即有
时,猜想成立,即有![]() , 9分
, 9分
则当![]() 时,有
时,有![]() ,
,
即当![]() 时猜想也成立, 13分
时猜想也成立, 13分
综合①②知,数列![]() 通项公式为
通项公式为![]() . 14分
. 14分
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生研究学习小组发现,学生上课的注意力指标随着听课时间的变化而变化,老师讲课开始时,学生的兴趣激增;接下来学生的兴趣将保持较理想的状态一段时间,随后学生的注意力开始分散.设
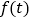 表示学生注意力指标.
表示学生注意力指标.该小组发现
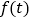 随时间
随时间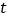 (分钟)的变化规律(
(分钟)的变化规律(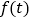 越大,表明学生的注意力越集中)如下:
越大,表明学生的注意力越集中)如下: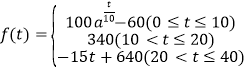 (
( 且
且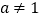 ).
).若上课后第
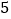 分钟时的注意力指标为
分钟时的注意力指标为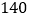 ,回答下列问题:
,回答下列问题:(
 )求
)求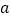 的值.
的值.(
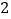 )上课后第
)上课后第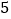 分钟和下课前
分钟和下课前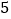 分钟比较,哪个时间注意力更集中?并请说明理由.
分钟比较,哪个时间注意力更集中?并请说明理由.(
 )在一节课中,学生的注意力指标至少达到
)在一节课中,学生的注意力指标至少达到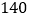 的时间能保持多长?
的时间能保持多长? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:集合
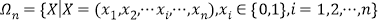 ,其中
,其中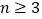 .
. ,称
,称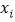 为
为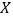 的第
的第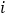 个坐标分量.若
个坐标分量.若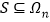 ,且满足如下两条性质:
,且满足如下两条性质:①
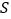 中元素个数不少于
中元素个数不少于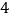 个.
个.②
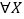 ,
,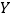 ,
, ,存在
,存在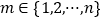 ,使得
,使得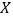 ,
,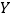 ,
,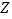 的第
的第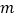 个坐标分量都是
个坐标分量都是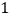 .则称
.则称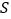 为
为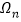 的一个好子集.
的一个好子集.(
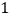 )若
)若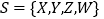 为
为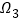 的一个好子集,且
的一个好子集,且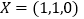 ,
,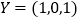 ,写出
,写出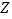 ,
,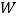 .
.(
 )若
)若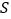 为
为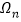 的一个好子集,求证:
的一个好子集,求证: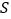 中元素个数不超过
中元素个数不超过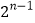 .
.(
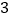 )若
)若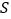 为
为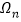 的一个好子集且
的一个好子集且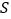 中恰好有
中恰好有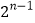 个元素,求证:一定存在唯一一个
个元素,求证:一定存在唯一一个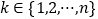 ,使得
,使得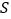 中所有元素的第
中所有元素的第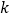 个坐标分量都是
个坐标分量都是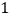 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
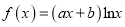 在
在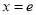 处的切线方程为
处的切线方程为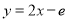
(1)求
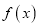 的解析式;
的解析式;(2)若对任意的
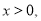 均有
均有 求实数k的取值范围;
求实数k的取值范围;(3)设
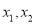 为两个正数,求证:
为两个正数,求证: 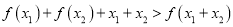
-
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}满足:a1=
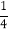 ,a2=
,a2=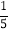 ,且a1a2+a2a3+…+anan+1=na1an+1对任何的正整数n都成立,则
,且a1a2+a2a3+…+anan+1=na1an+1对任何的正整数n都成立,则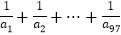 的值为( )
的值为( )A. 5032 B. 5044 C. 5048 D. 5050
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣a|+|x+5﹣a|
(1)若不等式f(x)﹣|x﹣a|≤2的解集为[﹣5,﹣1],求实数a的值;
(2)若x0∈R,使得f(x0)<4m+m2 , 求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, 是平面,
是平面, ,
, 是直线,给出下列命题:
是直线,给出下列命题:①若
 ,
, ,则
,则 ;
;②若
 ,
, ,
, ,
, ,则
,则 ;
;③如果
 ,
, ,
, ,
, 是异面直线,则
是异面直线,则 与
与 相交;
相交;④若
 .
. ,且
,且 ,
, ,则
,则 ,且
,且
其中正确确命题的序号是_____(把正确命题的序号都填上)
相关试题

