【题目】每逢节假日,在微信好友群中发红包逐渐成为一种时尚,还能增进彼此的感情,2016年春节期间,小鲁在自己的微信好友群中,向在线的甲、乙、丙、丁四位好友随机发放红包,发放的规则为:每次发放一个,小鲁自己不抢,每个人抢到的概率相同.
(1)若小鲁随机发放了3个红包,求甲至少抢到一个红包的概率;
(2)若丁因有事暂时离线一段时间,而小鲁在这段时间内共发了3个红包,其中2个红包中各有10元,一个红包中有5元.设这段时间内乙所得红包的总钱数为![]() 元,求随机变量
元,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
参考答案:
【答案】(1)![]() ;(2)分布列见解析,
;(2)分布列见解析, ![]() .
.
【解析】试题分析:(1)设“甲至少得![]() 红包”为事件
红包”为事件![]() ,利用
,利用![]() 次独立重复试验中事件
次独立重复试验中事件![]() 恰好发生
恰好发生![]() 次的概率计算公式能求出甲至少抢到一个红包的概率;(2)由题意知
次的概率计算公式能求出甲至少抢到一个红包的概率;(2)由题意知![]() 可能取值为
可能取值为![]() ,分别求出相应的概率,由此能求出随机变量
,分别求出相应的概率,由此能求出随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
试题解析:(1)设“甲至少得1红包”为事件![]() ,由题意得:
,由题意得:
![]() .
.
(2)由题意知![]() 可能取值为
可能取值为![]() ,
,
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
,
所以![]() 的分布列为
的分布列为

![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市出租车的现行计价标准是:路程在2 km以内(含2 km)按起步价8元收取,超过2 km后的路程按1.9 元/km收取,但超过10 km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85(元/km)).
(1)将某乘客搭乘一次出租车的费用f(x)(单位:元)表示为行程x(0<x≤60,单位:km)的分段函数;
(2)某乘客的行程为16 km,他准备先乘一辆出租车行驶8 km后,再换乘另一辆出租车完成余下行程,请问:他这样做是否比只乘一辆出租车完成全部行程更省钱?
(现实中要计等待时间且最终付费取整数,本题在计算时都不予考虑)
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校艺术节对同一类的
 ,
,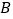 ,
,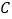 ,
,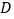 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:甲说:“是
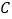 或
或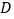 作品获得一等奖”;
作品获得一等奖”;乙说:“
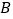 作品获得一等奖”;
作品获得一等奖”;丙说:“
 ,
,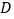 两项作品未获得一等奖”;
两项作品未获得一等奖”;丁说:“是
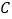 作品获得一等奖”.
作品获得一等奖”.若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一日能来回16次,如果每次拖7节车厢,则每日能来回10次.
(1)若每日来回的次数是车头每次拖挂车厢节数的一次函数,求此一次函数解析式:
(2)在(1)的条件下,每节车厢能载乘客110人.问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
(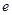 为自然对数的底数,
为自然对数的底数, ),
),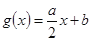 (
(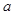 ,
,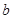
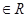 ),
),⑴若
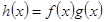 ,
,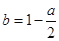 .求
.求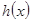 在
在 上的最大值
上的最大值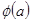 的表达式;
的表达式;⑵若
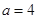 时,方程
时,方程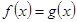 在
在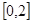 上恰有两个相异实根,求实根
上恰有两个相异实根,求实根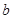 的取值范围;
的取值范围;⑶若
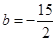 ,
,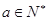 ,求使
,求使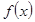 得图像恒在
得图像恒在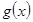 图像上方的最大正整数
图像上方的最大正整数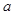 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某居民区随机抽取10个家庭,获得第
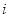 个家庭的月收入
个家庭的月收入 (单位:千元)与月储蓄
(单位:千元)与月储蓄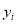 (单位:千元)的数据资料,算得
(单位:千元)的数据资料,算得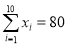 ,
, ,
,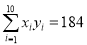 ,
,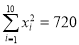 .
.(1)求家庭的月储蓄
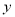 对月收入
对月收入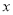 的线性回归方程
的线性回归方程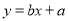 ;
;(2)判断变量
 与
与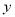 之间是正相关还是负相关;
之间是正相关还是负相关;(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
其中
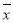 ,
, 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为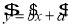
附:线性回归方程
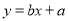 中,
中,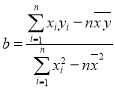 ,
,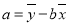 ,
, -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+y2=4,直线l:x+y=2.以O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系.
(1)将圆C和直线l的方程化为极坐标方程;
(2)P是l上的点,射线OP交圆C于点R,又点Q在OP上且满足|OQ|·|OP|=|OR|2,当点P在l上移动时,求点Q轨迹的极坐标方程.
相关试题

