搜索
【题目】已知函数f（x）=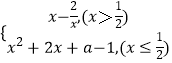 
（其中a＞0，a为常数），求函数f（x）的零点．
参考答案：
【答案】解：①x＞ 
时，f（x）=0，即x﹣ 
=0，解得x= 
；
②当x≤ 时，f（x）=x2+2ax+a﹣1，△=4﹣4（a﹣1）=8﹣4a，
当a＞2时，△＜0，f（x）=0无实根；
当a=2时，△=0，f（x）=0，解得x=﹣1
∵x∈（﹣∞， ]，
∴f（x）有一个零点﹣1
当0＜a＜2时，△＞0，x2+2ax+a﹣1=0，解得x=﹣1± 
，
∵﹣1﹣ ＜0＜ ，﹣1+ ＜﹣1+ ＜ ，
∴﹣1± 都是f（x）的零点．
综上所述，当a＞2时，f（x）的零点为： ；
当a=2时，f（x）的零点为： 和﹣1，
当0＜a＜2时，f（x）的零点为： 和﹣1+ ，﹣1﹣
【解析】根据分段函数和函数零点的定义，分类讨论，即可求出函数的零点．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知直线C1：
（ t 为参数），曲线C2： 
（r＞0，θ为参数）．（1）当r=1时，求C 1 与C2的交点坐标；
（2）点P 为曲线 C2上一动点，当r=
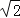时，求点P 到直线C1距离最大时点P 的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知y=f（x）是定义在R上的奇函数，且x＞0时，f（x）=1+（
）x
（1）求函数f（x）的解析式；
（2）画出函数f（x）的草图；
（3）利用图象直接写出函数f（x）的单调区间及值域． -
科目： 来源： 题型：
查看答案和解析>>【题目】知函数f（x）=ax2﹣2x+lnx（a≠0，a∈R）．
（1）判断函数 f （x）的单调性；
（2）若函数 f （x）有两个极值点x1，x2，求证：f（x1）+f（x2）＜﹣3．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两地相距200千米，汽车从甲地匀速行驶到乙地，速度不得超过50千米/时．已知汽车每小时的运输成本（以元为单位）由可变部分和固定部分组成：可变部分与速度v（千米/时）的平方成正比，比例系数为0.02；固定部分为50（元/时）．
（1）把全程运输成本y（元）表示为速度v（千米/时）的函数，并指出定义域；
（2）用单调性定义证明（1）中函数的单调性，并指出汽车应以多大速度行驶可使全程运输成本最小？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知f（x）=x2+bx+c（b，c∈R，b＜0）．
（1）若f（x）的定义域为[0，1]时，值域也是[0，1]，求b，c的值；
（2）若b=﹣2时，若函数g（x）=
对任意x∈[3，5]，g（x）＞c恒成立，试求实数c的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的方程x2﹣2alnx﹣2ax=0有唯一解，则实数a的值为（ ）
A.1
B.
C.
D.
相关试题
