
【题目】已知不等式|2x-1|+|2x-2|<x+3的解集是A.
(Ⅰ)求集合A;
(Ⅱ)设x,y∈A,对任意a∈R,求证:xy(||x+a|-|y+a||)<x2+y2.
【答案】(Ⅰ)A={x|0<x<2}(Ⅱ)见解析
【解析】
(Ⅰ)利用零点分类法,进行求解不等式;
(Ⅱ)利用绝对值不等式的性质和基本不等式进行证明。
解:(Ⅰ)当x<![]() 时,不等式变形为1-2x+2-2x<x+3,解得0<x<
时,不等式变形为1-2x+2-2x<x+3,解得0<x<![]() ;
;
当![]() 时,不等式变形为2x-1+2-2x<x+3,解得
时,不等式变形为2x-1+2-2x<x+3,解得![]() ;
;
当x>1时,不等式变形为2x-1+2x-2<x+3,解得1<x<2;
综上得A={x|0<x<2}.
(Ⅱ)∵x,y∈A,∴0<x,y<2,
∵||x+a|-|y+a||≤|(x+a)-(y+a)|=|x-y|,
∵0<x,y<2,∴-2<x-y<2,∴|x-y|<2,∴||x+a|-|y+a||<2,
∵![]() +
+![]() ≥2
≥2![]() =2,∴||x+a|-|y+a||<
=2,∴||x+a|-|y+a||<![]() +
+![]() ,即xy(|x+a|-|y+a|)<x2+y2.
,即xy(|x+a|-|y+a|)<x2+y2.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,左顶点为
,左顶点为![]() .过点
.过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程:
的方程:
(2)已知![]() 为
为![]() 的中点,是否存在定点
的中点,是否存在定点![]() ,对任意的直线
,对任意的直线![]() ,
,![]() 恒成立?若存在,求出点
恒成立?若存在,求出点![]() 的坐标;若不存在说明理由;
的坐标;若不存在说明理由;
(3)过![]() 点作直线
点作直线![]() 的平行线与椭圆
的平行线与椭圆![]() 相交,
相交,![]() 为其中一个交点,求
为其中一个交点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知城市![]() 周边有两个小镇
周边有两个小镇![]() 、
、![]() ,其中乡镇
,其中乡镇![]() 位于城市
位于城市![]() 的正东方
的正东方![]() 处,乡镇
处,乡镇![]() 与城市
与城市![]() 相距
相距![]() ,
,![]() 与
与![]() 夹角的正切值为2,为方便交通,现准备建设一条经过城市
夹角的正切值为2,为方便交通,现准备建设一条经过城市![]() 的公路
的公路![]() ,使乡镇
,使乡镇![]() 和
和![]() 分别位于
分别位于![]() 的两侧,过
的两侧,过![]() 和
和![]() 建设两条垂直
建设两条垂直![]() 的公路
的公路![]() 和
和![]() ,分别与公路
,分别与公路![]() 交汇于
交汇于![]() 、
、![]() 两点,以
两点,以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,建立如图所示的平面直角坐标系
轴,建立如图所示的平面直角坐标系![]() .
.
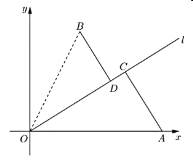
(1)当两个交汇点![]() 、
、![]() 重合,试确定此时
重合,试确定此时![]() 路段长度;
路段长度;
(2)当![]() ,计算此时两个交汇点
,计算此时两个交汇点![]() 、
、![]() 到城市
到城市![]() 的距离之比;
的距离之比;
(3)若要求两个交汇点![]() 、
、![]() 的距离不超过
的距离不超过![]() ,求
,求![]() 正切值的取值范围.
正切值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() ,
,![]() 是抛物线上的两个动点,且
是抛物线上的两个动点,且![]() ,过
,过![]() ,
,![]() 两点分别作抛物线的切线,设其交点为
两点分别作抛物线的切线,设其交点为![]() .
.
(1)若直线![]() 与
与![]() ,
,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,且
,且![]() 的面积为
的面积为![]() ,求
,求![]() 的值;
的值;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校今年高三毕业班报考飞行员学生的体重情况,将所得的数据整理后,画出了如图所示的频率分布直方图.已知图中从左到右的前三组的频率之比为1:2:3,其中体重在![]() 的有5人.
的有5人.

(1)求该校报考飞行员的总人数;
(2)从该校报考飞行员的体重在![]() 学生中任选3人,设
学生中任选3人,设![]() 表示体重超过70
表示体重超过70![]() 的学生人数,求
的学生人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
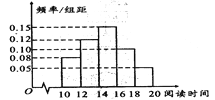
【题目】某教师将寒假期间该校所有学生阅读小说的时间统计如下图所示,并统计了部分学生阅读小说的类型,得到的数据如下表所示:
男生 | 女生 | |
阅读武侠小说 | 80 | 30 |
阅读都市小说 | 20 | 70 |
(1)是否有99.9%的把握认为“性别”与“阅读小说的类型”有关?
(2)求学生阅读小说时间的众数和平均数(同一组数据用该组区间的中点值作代表);
(3)若按照分层抽样的方法从阅读时间在![]() 、
、![]() 的学生中随机抽取6人,再从这6人中随机挑选2人介绍选取小说类型的缘由,求所挑选的2人阅读时间都在
的学生中随机抽取6人,再从这6人中随机挑选2人介绍选取小说类型的缘由,求所挑选的2人阅读时间都在![]() 的概率.
的概率.
附:![]() ,
,![]() .
.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
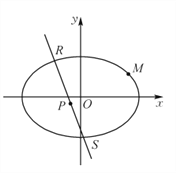
【题目】如图,椭圆![]() 经过点
经过点![]() ,且点
,且点![]() 到椭圆的两焦点的距离之和为
到椭圆的两焦点的距离之和为![]() .
.
(l)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是椭圆
是椭圆![]() 上的两个点,线段
上的两个点,线段![]() 的中垂线
的中垂线![]() 的斜率为
的斜率为![]() 且直线
且直线![]() 与
与![]() 交于点
交于点![]() ,
,![]() 为坐标原点,求证:
为坐标原点,求证:![]() 三点共线.
三点共线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com