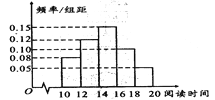
【题目】某教师将寒假期间该校所有学生阅读小说的时间统计如下图所示，并统计了部分学生阅读小说的类型，得到的数据如下表所示：

男生

女生

阅读武侠小说

80

30

阅读都市小说

20

70

（1）是否有99.9%的把握认为“性别”与“阅读小说的类型”有关？

（2）求学生阅读小说时间的众数和平均数（同一组数据用该组区间的中点值作代表）；

（3）若按照分层抽样的方法从阅读时间在、的学生中随机抽取6人，再从这6人中随机挑选2人介绍选取小说类型的缘由，求所挑选的2人阅读时间都在的概率.

附：，.

0.025

0.010

0.005

0.001

5.024

6.635

7.879

10.828

【答案】（1）见解析（2）众数为15，平均数为（3）.

【解析】

（1）通过公式计算求得，对比临界值表可得结果；（2）众数为最高矩形横坐标的中点；平均数为每个矩形横坐标中点与对应矩形面积乘积的总和，求解得到结果；（3）根据分层抽样可确定抽取的人阅读时间在的有人；阅读时间在的有人，列举出所有的情况和符合题意的情况，根据古典概型公式求得结果.

（1）由题意得，完善列联表如下：

男生

女生

总计

阅读武侠小说

阅读都市小说

总计

有的把握认为“性别”与“阅读小说的类型”有关

（2）由题意得，所求众数为；

所求平均数为

（3）由题意得，抽取的人阅读时间在的有人，记为；阅读时间在的有人，记为

则从人中挑选人，所有的情况共种，它们是：，

其中满足条件的有种：

故所求概率

关闭