【题目】设0<x<1,a>0且a≠1,试比较|loga(1-x)|与|loga(1+x)|的大小.
参考答案:
【答案】|loga(1-x)|>|loga(1+x)|
【解析】主要考查对数运算、对数函数的图象和性质。
解法一:作差法
|loga(1-x)|-|loga(1+x)|=|![]() |-|
|-|![]() |=
|=![]() (|lg(1-x)|-|lg(1+x)|)
(|lg(1-x)|-|lg(1+x)|)
∵0<x<1,∴0<1-x<1<1+x
∴上式=-![]() [(lg(1-x)+lg(1+x)]=-
[(lg(1-x)+lg(1+x)]=-![]() ·lg(1-x2)
·lg(1-x2)
由0<x<1,得,lg(1-x2)<0,∴-![]() ·lg(1-x2)>0,
·lg(1-x2)>0,
∴|loga(1-x)|>|loga(1+x)|
解法二:作商法
![]() =|log(1-x)(1+x)|
=|log(1-x)(1+x)|
∵0<x<1,∴0<1-x<1+x,∴|log(1-x)(1+x)|=-log(1-x)(1+x)=log(1-x)![]()
由0<x<1,∴1+x>1,0<1-x2<1
∴0<(1-x)(1+x)<1,∴![]() >1-x>0
>1-x>0
∴0<log(1-x) ![]() <log(1-x)(1-x)=1
<log(1-x)(1-x)=1
∴|loga(1-x)|>|loga(1+x)|
解法三:平方后比较大小
∵loga2(1-x)-loga2(1+x)=[loga(1-x)+loga(1+x)][loga(1-x)-loga(1+x)]
=loga(1-x2)·loga![]() =
=![]() ·lg(1-x2)·lg
·lg(1-x2)·lg![]()
∵0<x<1,∴0<1-x2<1,0<![]() <1
<1
∴lg(1-x2)<0,lg![]() <0
<0
∴loga2(1-x)>loga2(1+x),即|loga(1-x)|>|loga(1+x)|
解法四:分类讨论去掉绝对值
当a>1时,|loga(1-x)|-|loga(1+x)|=-loga(1-x)-loga(1+x)=-loga(1-x2)
∵0<1-x<1<1+x,∴0<1-x2<1
∴loga(1-x2)<0,∴-loga(1-x2)>0
当0<a<1时,由0<x<1,则有loga(1-x)>0,loga(1+x)<0
∴|loga(1-x)|-|loga(1+x)|=|loga(1-x)+loga(1+x)|=loga(1-x2)>0
∴当a>0且a≠1时,总有|loga(1-x)|>|loga(1+x)|
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC的三个内角为A,B,C,m=(sin B+sin C,0),n=(0,sin A)且
|m|2-|n|2=sin Bsin C.
(1)求角A的大小
(2)求sin B+sin C的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一医用放射性物质原来质量为a,每年衰减的百分比相同,当衰减一半时,所用时间是10年,根据需要,放射性物质至少要保留原来的,否则需要更换.已知到今年为止,剩余的为原来的
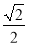 ,
,(1)求每年衰减的百分比;
(2)到今年为止,该放射性物质已衰减了多少年?
(3)今后至多还能用多少年?
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系
 的原点,极轴为
的原点,极轴为 轴的正半轴,两种坐标系中的长度单位相同,已知曲线
轴的正半轴,两种坐标系中的长度单位相同,已知曲线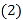 的极坐标方程为
的极坐标方程为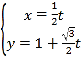 .
.(1)求
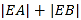 的直角坐标方程;
的直角坐标方程;(2)直线
 (
(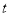 为参数)与曲线
为参数)与曲线 交于
交于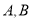 两点,与
两点,与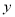 轴交于
轴交于 ,求
,求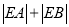 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前三项与数列{bn}的前三项相同,且a1+2a2+22a3+…+2n-1an=8n对任意n∈N*都成立,数列{bn+1-bn}是等差数列.
(1)求数列{an}与{bn}的通项公式;
(2)是否存在k∈N*,使得(bk-ak)∈(0,1)?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三个内角A、B、C所对的边分别是a、b、c,向量m=(cos B,cos C),n=(2a+c,b),且m⊥n.
(1)求角B的大小;
(2)若b=
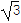 ,求a+c的取值范围.
,求a+c的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=b·ax(其中a,b为常量,且a>0,a≠1)的图象经过点A(1,6),B(3,24).
(1)求f(x);
(2)若不等式
 -m≥0在x∈(-∞,1]时恒成立,求实数m的取值范围.
-m≥0在x∈(-∞,1]时恒成立,求实数m的取值范围.
相关试题

