搜索
【题目】选修4-4：坐标系与参数方程
极坐标系的极点为直角坐标系
的原点，极轴为
轴的正半轴，两种坐标系中的长度单位相同，已知曲线
的极坐标方程为
.
（1）求
的直角坐标方程；
（2）直线
（
为参数）与曲线
交于
两点，与
轴交于
，求
.
参考答案：
【答案】（Ⅰ） (x－1)2＋(y－1)2＝2． （Ⅱ）|EA|＋|EB|＝
【解析】试题分析：（1）由极坐标和直角坐标之间的转换公式，即可求出结果；（2）将
的参数方程代入曲线C的直角坐标方程，化简得
，点E对应的参数
，设点A，B对应的参数分别为
，则
， 
，再根据
即可求出结果．
试题解析：（1）由
得
，得直角坐标方程为
，即
；
（2）将
的参数方程代入曲线C的直角坐标方程，化简得
，点E对应的参数
，设点A，B对应的参数分别为
，则
， 
，所以
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】现有4个人参加某娱乐活动，该活动有甲、乙两个游戏可供参加者选择，为增加趣味性，约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏，掷出点数为1或2的人去参加甲游戏，掷出点数大于2的人去参加乙游戏．
（1） 求出4个人中恰有2个人去 参加甲游戏的概率；
（2）求这4个人中去参加甲游戏人数大于去参加乙游戏的人数的概率；
（3）用
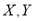分别表示这4个人中去参加甲、乙游戏的人数，记
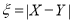,求随机变量
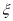的分布列与数学期望
． -
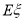科目： 来源： 题型：
查看答案和解析>>【题目】已知，△ABC的三个内角为A，B，C，m＝（sin B＋sin C,0），n＝（0，sin A）且
|m|2－|n|2＝sin Bsin C．
（1）求角A的大小
（2）求sin B＋sin C的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一医用放射性物质原来质量为a，每年衰减的百分比相同,当衰减一半时，所用时间是10年，根据需要,放射性物质至少要保留原来的，否则需要更换.已知到今年为止，剩余的为原来的
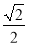，(1)求每年衰减的百分比；
(2)到今年为止，该放射性物质已衰减了多少年？
(3)今后至多还能用多少年？
-
科目： 来源： 题型：
查看答案和解析>>【题目】设0＜x＜1，a＞0且a≠1，试比较|loga(1－x)|与|loga(1＋x)|的大小．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知数列{an}的前三项与数列{bn}的前三项相同，且a1＋2a2＋22a3＋…＋2n－1an＝8n对任意n∈N*都成立，数列{bn＋1－bn}是等差数列．
（1）求数列{an}与{bn}的通项公式；
（2）是否存在k∈N*，使得（bk－ak）∈（0,1）？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC的三个内角A、B、C所对的边分别是a、b、c，向量m＝(cos B，cos C)，n＝(2a＋c，b)，且m⊥n.
(1)求角B的大小；
(2)若b＝
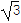，求a＋c的取值范围．
相关试题
