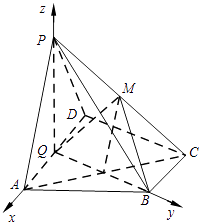
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC= ![]() AD=1,CD=
AD=1,CD= ![]() .
. 
(1)求证:平面PQB⊥平面PAD;
(2)若M为棱PC的中点,求异面直线AP与BM所成角的余弦值;
(3)若二面角M﹣BQ﹣C大小为30°,求QM的长.
参考答案:
【答案】
(1)解:∵AD∥BC,BC= ![]() AD,Q为AD的中点,
AD,Q为AD的中点,
∴四边形BCDQ为平行四边形,∴CD∥BQ
又∵∠ADC=90°,∴∠AQB=90° 即QB⊥AD.
又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.∵BQ平面PQB,
∴平面PQB⊥平面PAD.
(2)解:∵PA=PD,Q为AD的中点,∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系.
则Q(0,0,0),A(1,0,0), ![]() ,
, ![]() ,C(﹣1,
,C(﹣1, ![]() ,0)
,0)
∵M是PC中点,∴ ![]() ,
,
∴ ![]()
设异面直线AP与BM所成角为θ
则cosθ= 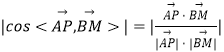 =
= ![]() ,
,
∴异面直线AP与BM所成角的余弦值为 ![]() ;
;
(3)解:由(2)知平面BQC的法向量为 ![]() ,
,
由 ![]() ,且0≤λ≤1,得
,且0≤λ≤1,得 ![]() ,
,
又 ![]() ,∴平面MBQ法向量为
,∴平面MBQ法向量为 ![]() .
.
∵二面角M﹣BQ﹣C为30°,∴ 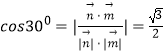 ,
,
∴ ![]() .∴|QM|=
.∴|QM|= ![]()
【解析】(1)由题意易证QB⊥AD,由面面垂直的性质可得BQ⊥平面PAD,可得结论;(2)易证PQ⊥平面ABCD,以Q为原点建立空间直角坐标系,则可得相关点的坐标,可得向量 ![]() 和
和 ![]() 的坐标,可得夹角的余弦值,由反三角函数可得答案;(3)可得平面BQC的法向量为
的坐标,可得夹角的余弦值,由反三角函数可得答案;(3)可得平面BQC的法向量为 ![]() ,又可求得平面MBQ法向量为
,又可求得平面MBQ法向量为 ![]() ,结合题意可得λ的方程,解方程可得λ,可得所求.
,结合题意可得λ的方程,解方程可得λ,可得所求.
【考点精析】本题主要考查了异面直线及其所成的角和平面与平面垂直的判定的相关知识点,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义max{a,b}表示实数a,b中的较大的数.已知数列{an}满足a1=a(a>0),a2=1,an+2=
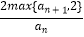 (n∈N),若a2015=4a,记数列{an}的前n项和为Sn , 则S2015的值为 .
(n∈N),若a2015=4a,记数列{an}的前n项和为Sn , 则S2015的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,圆
中,圆 的方程为
的方程为 ,若直线
,若直线 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆 有公共点,则
有公共点,则 的最大值为__________.
的最大值为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】网上购物逐步走进大学生活,某大学学生宿舍4人积极参加网购,大家约定:每个人通过掷一枚质地均匀的骰子决定自己去哪家购物,掷出点数为5或6的人去淘宝网购物,掷出点数小于5的人去京东商场购物,且参加者必须从淘宝和京东商城选择一家购物.
(1)求这4人中恰有1人去淘宝网购物的概率;
(2)用ξ、η分别表示这4人中去淘宝网和京东商城购物的人数,记X=ξη,求随机变量X的分布列与数学期望EX. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:(a-1)x+y+b=0,l2:ax+by-4=0,求满足下列条件的a,b的值.
(1)l1⊥l2,且l1过点(1,1);
(2)l1∥l2,且l2在第一象限内与两坐标轴围成的三角形的面积为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.

(1)求四面体ABCD的体积;
(2)证明:四边形EFGH是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 的右焦点为F(1,0),且点(﹣1,
的右焦点为F(1,0),且点(﹣1,  )在椭圆C上.
)在椭圆C上.
(1)求椭圆C的标准方程;
(2)已知动直线l过点F,且与椭圆C交于A,B两点,试问x轴上是否存在定点Q,使得 恒成立?若存在,求出点Q的坐标,若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标,若不存在,请说明理由.
相关试题

