【题目】已知函数f(x)=ax2+bx+c(a>0,b∈R,c∈R).
(1)若函数f(x)的最小值是f(﹣1)=0,且c=1,求f (2)的值;
(2)若a=1,c=0,且|f(x)|≤1在区间(0,1]上恒成立,试求b的取值范围.
参考答案:
【答案】(1)9 ; (2)[﹣2,![]() ].
].
【解析】
(1)根据函数f(x)的最小值是f(﹣1)=0,且c=1,求解得a,b,即可求解f (2)的值;
(2)将a=1,c=0代入,|f(x)|≤1在区间(0,1]上恒成立,转化为不等式问题求解即可.
函数f(x)=ax2+bx+c(a>0,b∈R,c∈R).
(1)由题意,可得![]() ,a﹣b+1=0,
,a﹣b+1=0,
解得:a=1,b=2;
∴函数f(x)=x2+2x+1.
那么f(2)=4+4+1=9;
(2)由a=1,c=0,可得f(x)=x2+bx;
∵|f(x)|≤1在区间(0,1]上恒成立,
即|x2+bx|≤1
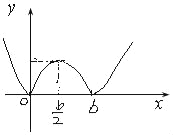
令g(x)=|x2+bx|=|x(x+b)|,显然图象过原点,(b,0).
当b<0,g(x)在区间(0,1]上单调递增,可得g(x)的图象,(如图)
g(x)max=g(1)=|b+1|≤1
∴﹣2≤b<0
当b=0时,可得|x2|≤1在区间(0,1]上恒成立,
可得:﹣2≤b≤0;
当b>0,显然g(x)max=![]()
解得:![]() ≥b>0
≥b>0
综上可得b的取值范围是[﹣2,![]() ].
].
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=2x,g(x)是一次函数,并且点(2,2)在函数f[(g(x)]的图象上,点(2,5)在函数g[f(x)]的图象上,则g(x)的解析式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图给出了一个程序框图,其作用是输入x的值,输出相应的y值.若要使输入的x值与输出的y值相等,则这样的x值有( )
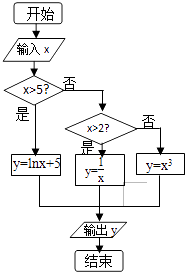
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】设P(x0,y0)是函数f(x)图象上任意一点,且y02≥x02,则f(x)的解析式可以是_____.(填序号)
①f(x)=x﹣
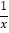 ②f(x)=ex﹣1(e≈2.718,是一个重要常数)③f(x)=x+
②f(x)=ex﹣1(e≈2.718,是一个重要常数)③f(x)=x+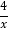 ④y=x2
④y=x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}的前n项和为Sn , 且S2=11,S5=50,则过点P(n,an)和Q(n+2,an+2)(n∈N*)的直线的一个方向向量的坐标可以是( )
A.(﹣1,﹣3)
B.(1,﹣3)
C.(1,1)
D.(1,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,四边形
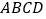 中,
中,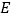 是
是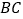 的中点,
的中点, 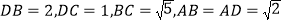 .将(图甲)沿直线
.将(图甲)沿直线 折起,使二面角
折起,使二面角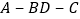 为
为 (如图乙).
(如图乙). (1)求证:
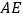 ⊥平面
⊥平面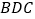
(2)求点
 到平面
到平面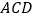 的距离.
的距离.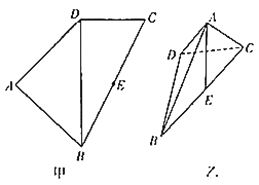
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在底面为正方形的四棱锥P-ABCD中,侧棱PD⊥底面ABCD,PD=DC,点E是线段PC的中点.

(1)求异面直线AP与BE所成角的大小;
(2)若点F在线段PB上,使得二面角F-DE-B的正弦值为
 ,求
,求 的值.
的值.
相关试题

