【题目】定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M≥0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的一个上界.已知函数f(x)=1+a( ![]() )x+(
)x+( ![]() )x , 若函数f(x)在[﹣2,1]上是以3为上界的有界函数,求实数a的取值范围.
)x , 若函数f(x)在[﹣2,1]上是以3为上界的有界函数,求实数a的取值范围.
参考答案:
【答案】解:由题意知,|f(x)|≤3在[﹣2,1]上恒成立.
所以﹣3≤f(x)≤3,即 ![]() .
.
∴ ![]() 在[﹣2,1]上恒成立.
在[﹣2,1]上恒成立.
∴ 
设2x=t, ![]() ,
, ![]() ,由x∈[﹣2,1]得
,由x∈[﹣2,1]得 ![]() ,
,
则h(t)在 ![]() 上的最大值为
上的最大值为 ![]() ,
,
p(t)在 ![]() 上的最小值为
上的最小值为 ![]() .
.
所以实数a的取值范围为 ![]()
【解析】利用定义得到|f(x)|≤3在[﹣2,1]上恒成立.化简为 ![]() 在[﹣2,1]上恒成立.设2x=t,
在[﹣2,1]上恒成立.设2x=t, ![]() ,
, ![]() ,求解不等式两端函数的最值,即可得到实数a的取值范围.
,求解不等式两端函数的最值,即可得到实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】轮船
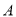 从某港口将一些物品送到正航行的轮船
从某港口将一些物品送到正航行的轮船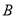 上,在轮船
上,在轮船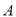 出发时,轮船
出发时,轮船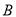 位于港口
位于港口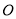 北偏西
北偏西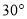 且与
且与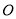 相距20海里的
相距20海里的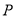 处,并正以30海里的航速沿正东方向匀速行驶,假设轮船
处,并正以30海里的航速沿正东方向匀速行驶,假设轮船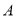 沿直线方向以
沿直线方向以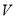 海里/小时的航速匀速行驶,经过
海里/小时的航速匀速行驶,经过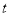 小时与轮船
小时与轮船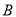 相遇.
相遇.(1)若使相遇时轮船
 航距最短,则轮船
航距最短,则轮船 的航行速度大小应为多少?
的航行速度大小应为多少?(2)假设轮船
 的最高航速只能达到30海里/小时,则轮船
的最高航速只能达到30海里/小时,则轮船 以多大速度及什么航行方向才能在最短时间与轮船
以多大速度及什么航行方向才能在最短时间与轮船 相遇,并说明理由.
相遇,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
 是边长为3的正方形,
是边长为3的正方形,  平面
平面 与平面
与平面 所成角为
所成角为 .
.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)设点
 是线段
是线段 上一个动点,试确定点
上一个动点,试确定点 的位置,使得
的位置,使得 平面
平面 ,并证明你的结论.
,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
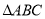 中,
中, 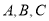 成等差数列是
成等差数列是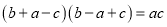 的( )
的( )A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,正确的个数是( )
①={0};②{0};③∈{0};④0={0};⑤0∈{0};⑥{1}∈{1,2,3};⑦{1,2}{1,2,3};⑧{a,b}={b,a}.
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组函数中,表示同一函数的是( )
A.f(x)=x﹣1,g(x)= ﹣1
﹣1
B.f(x)=|x|,g(x)=( )2
)2
C.f(x)=x,g(x)=
D.f(x)=2x,g(x)=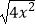
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大理石工厂初期花费98万元购买磨大理石刀具,第一年需要各种费用12万元,从第二年起,每年所需费用比上一年增加4万元,该大理石加工厂每年总收入50万元.
(1)到第几年末总利润最大,最大值是多少?
(2)到第几年末年平均利润最大,最大值是多少?
相关试题

