【题目】轮船![]() 从某港口将一些物品送到正航行的轮船
从某港口将一些物品送到正航行的轮船![]() 上,在轮船
上,在轮船![]() 出发时,轮船
出发时,轮船![]() 位于港口
位于港口![]() 北偏西
北偏西![]() 且与
且与![]() 相距20海里的
相距20海里的![]() 处,并正以30海里的航速沿正东方向匀速行驶,假设轮船
处,并正以30海里的航速沿正东方向匀速行驶,假设轮船![]() 沿直线方向以
沿直线方向以![]() 海里/小时的航速匀速行驶,经过
海里/小时的航速匀速行驶,经过![]() 小时与轮船
小时与轮船![]() 相遇.
相遇.
(1)若使相遇时轮船![]() 航距最短,则轮船
航距最短,则轮船![]() 的航行速度大小应为多少?
的航行速度大小应为多少?
(2)假设轮船![]() 的最高航速只能达到30海里/小时,则轮船
的最高航速只能达到30海里/小时,则轮船![]() 以多大速度及什么航行方向才能在最短时间与轮船
以多大速度及什么航行方向才能在最短时间与轮船![]() 相遇,并说明理由.
相遇,并说明理由.
参考答案:
【答案】(1)轮船![]() 以
以![]() 海里/小时的速度航行,相遇时轮船
海里/小时的速度航行,相遇时轮船![]() 航距最短;(2)航向为北偏东
航距最短;(2)航向为北偏东![]() ,航速为30海里/小时,轮船
,航速为30海里/小时,轮船![]() 能在最短时间与轮船
能在最短时间与轮船![]() 相遇.
相遇.
【解析】试题分析:(1)设两轮船在![]() 处相遇,在
处相遇,在![]() 中,利用余弦定理得出
中,利用余弦定理得出![]() 关于t的函数,从而得出
关于t的函数,从而得出![]() 的最小值及其对应的
的最小值及其对应的![]() ,得出速度;
,得出速度;
(2)利用余弦定理计算航行时间![]() ,得出
,得出![]() 距离,从而得出
距离,从而得出![]() 的度数,得出航行方案.
的度数,得出航行方案.
试题解析:(1)设相遇时轮船![]() 航行的距离为
航行的距离为![]() 海里,则
海里,则
![]()
![]()
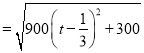 .
.
∴当![]() 时,
时, ![]() ,
, 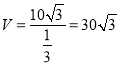 ,
,
即轮船![]() 以
以![]() 海里/小时的速度航行,相遇时轮船
海里/小时的速度航行,相遇时轮船![]() 航距最短.
航距最短.
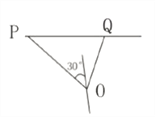
(2)设轮船![]() 与轮船
与轮船![]() 在
在![]() 处相遇,则
处相遇,则![]()
![]() ,
,
即![]() .
.
∵![]() ,
,
∴![]() ,即
,即![]() ,解得
,解得![]() ,又
,又![]() 时
时![]() ,
,
∴![]() 时,
时, ![]() 最小且为
最小且为![]() ,此时
,此时![]() 中
中![]() ,
,
∴航向为北偏东![]() ,航速为30海里/小时,
,航速为30海里/小时,
轮船![]() 能在最短时间与轮船
能在最短时间与轮船![]() 相遇.
相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,直线
中,直线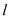 的参数方程为
的参数方程为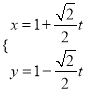 (
(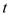 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以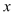 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆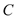 的极坐标方程为
的极坐标方程为 ,圆
,圆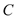 与直线
与直线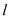 交于
交于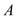 ,
,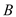 两点,
两点,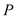 点的直角坐标为
点的直角坐标为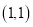 .
.(1)将直线
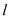 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆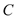 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;(2)求
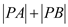 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数f(x)=x2+bx+c满足f(2)=f(﹣2),且函数的f(x)的一个根为1.
(1)求函数f(x)的解析式;
(2)对任意的x∈[ ,+∞),方程4mf(x)+f(x﹣1)=4﹣4m有解,求实数m的取值范围.
,+∞),方程4mf(x)+f(x﹣1)=4﹣4m有解,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】轮船
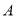 从某港口将一些物品送到正航行的轮船
从某港口将一些物品送到正航行的轮船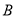 上,在轮船
上,在轮船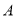 出发时,轮船
出发时,轮船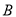 位于港口
位于港口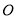 北偏西
北偏西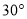 且与
且与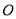 相距20海里的
相距20海里的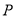 处,并正以30海里的航速沿正东方向匀速行驶,假设轮船
处,并正以30海里的航速沿正东方向匀速行驶,假设轮船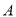 沿直线方向以
沿直线方向以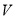 海里/小时的航速匀速行驶,经过
海里/小时的航速匀速行驶,经过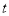 小时与轮船
小时与轮船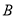 相遇.
相遇.(1)若使相遇时轮船
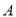 航距最短,则轮船
航距最短,则轮船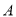 的航行速度大小应为多少?
的航行速度大小应为多少?(2)假设轮船
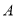 的最高航速只能达到30海里/小时,则轮船
的最高航速只能达到30海里/小时,则轮船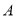 以多大速度及什么航行方向才能在最短时间与轮船
以多大速度及什么航行方向才能在最短时间与轮船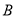 相遇,并说明理由.
相遇,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
 是边长为3的正方形,
是边长为3的正方形,  平面
平面 与平面
与平面 所成角为
所成角为 .
.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)设点
 是线段
是线段 上一个动点,试确定点
上一个动点,试确定点 的位置,使得
的位置,使得 平面
平面 ,并证明你的结论.
,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
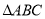 中,
中, 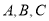 成等差数列是
成等差数列是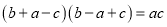 的( )
的( )A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在D上的函数f(x),如果满足:对任意x∈D,存在常数M≥0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的一个上界.已知函数f(x)=1+a(
 )x+(
)x+(  )x , 若函数f(x)在[﹣2,1]上是以3为上界的有界函数,求实数a的取值范围.
)x , 若函数f(x)在[﹣2,1]上是以3为上界的有界函数,求实数a的取值范围.
相关试题

