【题目】如图, ![]() 中,
中, ![]() 是
是![]() 的中点,
的中点, ![]() ,
, ![]() .将
.将![]() 沿
沿
![]() 折起,使
折起,使![]() 点与图中
点与图中![]() 点重合.
点重合.
(Ⅰ)求证:![]() ;
;
(Ⅱ)当三棱锥![]() 的体积取最大时,求二面角
的体积取最大时,求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在(Ⅱ)的条件下,试问在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?证明你的结论.
?证明你的结论.
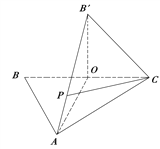
参考答案:
【答案】(Ⅰ)![]() 点,
点,
![]() 即
即![]() ,
,
又∵![]() ;
;
(Ⅱ)![]() ;(Ⅲ)存在,且为线段
;(Ⅲ)存在,且为线段![]() 的中点
的中点
证明如下:设![]() ,
,
![]()
又平面![]() 的法向量
的法向量![]() ,依题意得
,依题意得
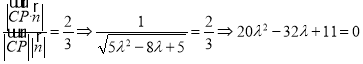
解得![]() 舍去).
舍去).
【解析】试题分析:(Ⅰ)欲证![]() ,需证明
,需证明![]() 垂直平面
垂直平面![]() 内两条直线,
内两条直线,
在三角形ABC中,因为![]() ,
, ![]() 是
是![]() 的中点,所以
的中点,所以![]() ;
;
又因为在折叠的过程中,![]() 保持不变,即
保持不变,即![]() ,
,![]() ,
,
所以结论成立;
(Ⅱ)在平面![]() 内,作
内,作![]() 于点
于点![]() ,则由(1)及已知可得当
,则由(1)及已知可得当![]() 与
与![]() 重合时,三棱锥
重合时,三棱锥![]() 的体积最大,并过
的体积最大,并过![]() 点作
点作![]() 于点
于点![]() ,连
,连![]() ,则
,则![]() 为
为![]()
在![]() 中,易得
中,易得![]() 的值,即为所求;
的值,即为所求;
(Ⅲ)根据图形及已知条件分析可得,存在线段![]() 上中点
上中点![]() ,使
,使![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求出平面
,求出平面![]() 的法向量
的法向量![]() ,根据
,根据![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() 建立等式关系,即可求得结论.
建立等式关系,即可求得结论.

试题解析:(Ⅰ) ![]() 点,
点,
![]() 即
即![]() ,
,
又∵![]() ;
;
(Ⅱ)在平面![]() 内,作
内,作![]() 于点
于点![]() ,则由(Ⅰ)可知
,则由(Ⅰ)可知![]()
又![]() ,
, ![]() ,即
,即![]() 是三棱锥
是三棱锥![]() 的高,
的高,
又![]() ,所以当
,所以当![]() 与
与![]() 重合时,三棱锥
重合时,三棱锥![]() 的体积最大,
的体积最大,
过![]() 点作
点作![]() 于点
于点![]() ,连
,连![]() ,由(Ⅰ)知
,由(Ⅰ)知
![]() ,
, ![]()
![]()
![]() 为
为![]()
![]() ,
, ![]()
![]()
(Ⅲ)存在,且为线段![]() 的中点
的中点
证明如下:设![]() ,
,
![]()
又平面![]() 的法向量
的法向量![]() ,依题意得
,依题意得
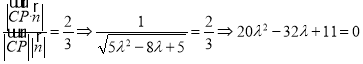
解得![]() 舍去).
舍去).
-
科目: 来源: 题型:
查看答案和解析>>【题目】满足{1}X{1,2,3,4}的集合X有( )
A.4个B.5个C.6个D.7个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产一批
 产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批
产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批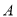 产品所需原材料减少了
产品所需原材料减少了 吨,且每吨原材料创造的利润提高了
吨,且每吨原材料创造的利润提高了 ;若将少用的
;若将少用的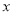 吨原材料全部用于生产公司新开发的
吨原材料全部用于生产公司新开发的 产品,每吨原材料创造的利润为
产品,每吨原材料创造的利润为 万元,其中
万元,其中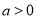 .
.(1)若设备升级后生产这批
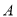 产品的利润不低于原来生产该批
产品的利润不低于原来生产该批 产品的利润,求
产品的利润,求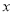 的取值范围;
的取值范围;(2)若生产这批
 产品的利润始终不高于设备升级后生产这批
产品的利润始终不高于设备升级后生产这批 产品的利润,求
产品的利润,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 平面
平面 ,
, ,
, ,
, 为
为 中点.
中点.
(1)求证:
 平面
平面 ;
;(2)求二面角
 的正弦值;
的正弦值;(3)求点
 到平面
到平面 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:
 ,直线l:
,直线l: 

(Ⅰ)求直线l所过定点A的坐标;
(Ⅱ)求直线l被圆C所截得的弦长最短时m的值及最短弦长;
(Ⅲ)已知点
 ,在直线MC上(C为圆心),存在定点N(异于点M),满足:对于圆C上任一点P,都有
,在直线MC上(C为圆心),存在定点N(异于点M),满足:对于圆C上任一点P,都有 为一常数,试求所有满足条件的点N的坐标及该常数。
为一常数,试求所有满足条件的点N的坐标及该常数。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
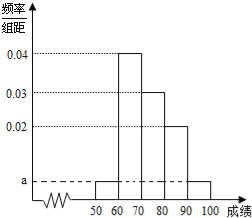
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如表所示,求数学成绩在[50,90)之外的人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业.根据规划,本年度投入
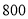 万元,以后每年投入将比上年减少
万元,以后每年投入将比上年减少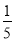 .本年度当地旅游业收入估计为
.本年度当地旅游业收入估计为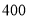 万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加
万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加 .
.(Ⅰ)设
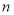 年内(本年度为第一年)总投入为
年内(本年度为第一年)总投入为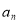 万元,旅游业总收入为
万元,旅游业总收入为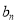 万元.写出
万元.写出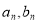 的表达式;
的表达式;(Ⅱ)至少经过几年旅游业的总收入才能超过总投入?
相关试题

