【题目】已知A(x1 , y1),B(x2 , y2)是函数f(x)= 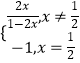 的图象上的任意两点(可以重合),点M在直线x=
的图象上的任意两点(可以重合),点M在直线x= ![]() 上,且
上,且 ![]() =
= ![]() .
.
(1)求x1+x2的值及y1+y2的值;
(2)已知S1=0,当n≥2时,Sn=f( ![]() )+f(
)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() ),求Sn .
),求Sn .
参考答案:
【答案】
(1)解:∵点M在直线x= ![]() 上,设M
上,设M ![]() .
.
又 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴x1+x2=1.
①当x1= ![]() 时,x2=
时,x2= ![]() ,y1+y2=f(x1)+f(x2)=﹣1﹣1=﹣2;
,y1+y2=f(x1)+f(x2)=﹣1﹣1=﹣2;
②当x1≠ ![]() 时,x2≠
时,x2≠ ![]() .
.
y1+y2= ![]() +
+ ![]() =
= ![]() =
= ![]() =
= ![]() =﹣2.
=﹣2.
综合①②得,y1+y2=﹣2.
(2)解:由(1)知,当x1+x2=1.y1+y2=﹣2.
∴ ![]() +
+ ![]() =﹣2,k=1,2,3,…,n﹣1.)
=﹣2,k=1,2,3,…,n﹣1.)
n≥2时,Sn=f ![]() +f
+f ![]() +…+f
+…+f ![]() ,①
,①
∴Sn= ![]() +
+ ![]() +…+
+…+ ![]() ,②
,②
①+②得,2Sn=﹣2(n﹣1),则Sn=1﹣n.
当n=1时,S1=0满足Sn=1﹣n.
∴Sn=1﹣n.
【解析】(1)点M在直线x= ![]() 上,设M
上,设M ![]() .又
.又 ![]() =
= ![]() ,利用坐标运算x1+x2=1.①当x1=
,利用坐标运算x1+x2=1.①当x1= ![]() 时,x2=
时,x2= ![]() ,y1+y2=f(x1)+f(x2);②当x1≠
,y1+y2=f(x1)+f(x2);②当x1≠ ![]() 时,x2≠
时,x2≠ ![]() .y1+y2=
.y1+y2= ![]() +
+ ![]() 化简即可得出.(2)由(1)知,当x1+x2=1.y1+y2=﹣2.可得
化简即可得出.(2)由(1)知,当x1+x2=1.y1+y2=﹣2.可得 ![]() +
+ ![]() =﹣2,k=1,2,3,…,n﹣1.即可得出.
=﹣2,k=1,2,3,…,n﹣1.即可得出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 【2017四川宜宾二诊】选修4-4:坐标系与参数方程
在直角坐标系
 中,已知点
中,已知点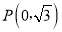 ,曲线
,曲线 的参数方程为
的参数方程为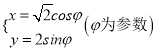 .以原点为极点,
.以原点为极点, 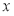 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线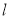 的极坐标方程为
的极坐标方程为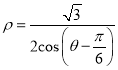 .
. (Ⅰ)判断点
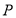 与直线
与直线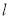 的位置关系并说明理由;
的位置关系并说明理由; (Ⅱ)设直线
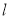 与曲线
与曲线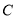 的两个交点分别为
的两个交点分别为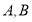 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017江西南昌十所重点二模】选修4—4:坐标系与参数方程
在平面直角坐标系xOy中,曲线C1的参数方程为
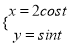 (t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:
(t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2: 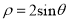 .
.(Ⅰ)求曲线C1和C2的直角坐标方程,并分别指出其曲线类型;
(Ⅱ)试判断:曲线C1和C2是否有公共点?如果有,说明公共点的个数;如果没有,请说明理由;
(Ⅲ)设
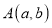 是曲线C1上任意一点,请直接写出a + 2b的取值范围.
是曲线C1上任意一点,请直接写出a + 2b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在四面体ABCD中,E、F分别是AC、BD的中点,若CD=2AB=4,EF⊥AB,则EF与CD所成的角为( )
A.90°
B.45°
C.60°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】为了得到函数y=cos(
 x+
x+  )的图象,只要把y=cos
)的图象,只要把y=cos  x的图象上所有的点( )
x的图象上所有的点( )
A.向左平移 个单位长度
个单位长度
B.向右平移 个单位长度
个单位长度
C.向左平移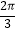 个单位长度
个单位长度
D.向右平移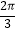 个单位长度
个单位长度 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )
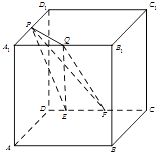
A.点P到平面QEF的距离
B.三棱锥P﹣QEF的体积
C.直线PQ与平面PEF所成的角
D.二面角P﹣EF﹣Q的大小 -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017安徽淮北二模】选修4—4:坐标系与参数方程
在直角坐标系
 中, 以
中, 以 为极点,
为极点, 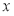 轴正半轴为极轴建立极坐标系, 圆
轴正半轴为极轴建立极坐标系, 圆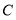 的极坐标方程为
的极坐标方程为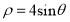 ,直线
,直线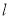 的参数方程为
的参数方程为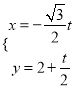 (t为参数), 直线
(t为参数), 直线 和圆
和圆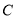 交于
交于 两点。
两点。(Ⅰ)求圆心的极坐标;
(Ⅱ)直线
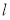 与
与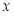 轴的交点为
轴的交点为 ,求
,求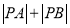 .
.
相关试题

