【题目】若对任意的x∈[﹣1,2],都有x2﹣2x+a≤0(a为常数),则a的取值范围是( )
A.(﹣∞,﹣3]
B.(﹣∞,0]
C.[1,+∞)
D.(﹣∞,1]
参考答案:
【答案】A
【解析】解:若对任意的x∈[﹣1,2],都有x2﹣2x+a≤0(a为常数)
对任意的x∈[﹣1,2],a≤﹣x2+2x(a为常数),
令f(x)=﹣x2+2x,x∈[﹣1,2],
由f(x)的对称轴x=1,得:f(x)在[﹣1,1)递增,在(1,2]递减,
∴f(x)min=f(﹣1)=﹣3,
∴a≤﹣3,
故选:A.
【考点精析】掌握二次函数的性质是解答本题的根本,需要知道当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(﹣4,4)、B(4,4),直线AM与BM相交于点M,且直线AM的斜率与直线BM的斜率之差为﹣2,点M的轨迹为曲线C.
(1)求曲线C 的轨迹方程;
(2)Q为直线y=﹣1上的动点,过Q做曲线C的切线,切点分别为D、E,求△QDE的面积S的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙C经过点A(﹣2,0),B(0,2),且圆心C在直线y=x上,直线L:y=kx+1与⊙C相交于P,Q点.
(1)求⊙C的方程.
(2)过点(0,1)作直线L1⊥L,且L1交⊙C于M,N,求四边形PMQN的面积最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=B=R,x∈A,y∈B,f:x→y=ax+b是从A到B的映射,若1和8的原象分别是3和10,则5在f下的象是( )
A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=ax2+2(a﹣3)x+1在区间[﹣2,+∞)上递减,则实数a的取值范围是( )
A.(﹣∞,﹣3]
B.[﹣3,0]
C.[﹣3,0)
D.[﹣2,0] -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:
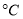 )有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间
)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间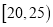 ,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温
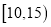
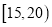
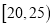
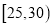
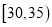
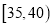
天数
2
16
36
25
7
4
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量
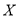 (单位:瓶)的分布列;
(单位:瓶)的分布列;(2)设六月份一天销售这种酸奶的利润为
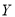 (单位:元).当六月份这种酸奶一天的进货量(单位:瓶)为多少时,
(单位:元).当六月份这种酸奶一天的进货量(单位:瓶)为多少时, 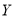 的数学期望达到最大值?
的数学期望达到最大值? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=e1+|x|﹣
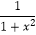 ,则使得f(x)>f(2x﹣1)成立的x的取值范围是( )
,则使得f(x)>f(2x﹣1)成立的x的取值范围是( )
A.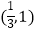
B.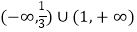
C.(﹣ ,
,  )
)
D.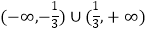
相关试题

