【题目】已知点A(﹣4,4)、B(4,4),直线AM与BM相交于点M,且直线AM的斜率与直线BM的斜率之差为﹣2,点M的轨迹为曲线C.
(1)求曲线C 的轨迹方程;
(2)Q为直线y=﹣1上的动点,过Q做曲线C的切线,切点分别为D、E,求△QDE的面积S的最小值.
参考答案:
【答案】(1)![]()
![]() (2)最小值4
(2)最小值4
【解析】试题分析:(Ⅰ)设![]() ,由题意得
,由题意得![]() ,化简可得曲线
,化简可得曲线![]() 的方程为
的方程为![]()
![]() ; (Ⅱ)设
; (Ⅱ)设![]() ,切线方程为
,切线方程为![]() ,与抛物线方程联立互为
,与抛物线方程联立互为![]() ,由于直线与抛物线相切可得
,由于直线与抛物线相切可得![]() ,解得
,解得![]() ,可切点
,可切点![]() ,由
,由![]() ,利用韦达定理,得到
,利用韦达定理,得到![]() ,得到
,得到![]() 为直角三角形,得出三角形面积的表达式,即可求解三角形的最小值.
为直角三角形,得出三角形面积的表达式,即可求解三角形的最小值.
试题解析:(Ⅰ)设M(x,y),由题意可得: ![]() ,
,
化为x2=4y.
∴曲线C 的轨迹方程为x2=4y且(x≠±4).
联立![]() ,化为x2﹣4kx+4(km+1)=0,
,化为x2﹣4kx+4(km+1)=0,
由于直线与抛物线相切可得△=0,即k2﹣km﹣1=0.
∴x2﹣4kx+4k2=0,解得x=2k.可得切点(2k,k2),
由k2﹣km﹣1=0.∴k1+k2=m,k1k2=﹣1.
∴切线QD⊥QE.
∴△QDE为直角三角形, ![]() |QD||QE|.
|QD||QE|.
令切点(2k,k2)到Q的距离为d,
则d2=(2k﹣m)2+(k2+1)2=4(k2﹣km)+m2+(km+2)2=4(k2﹣km)+m2+k2m2+4km+4=(4+m2)(k2+1),
∴|QD|=![]() ,
,
|QE|=![]() ,
,
∴![]() (4+m2)
(4+m2)![]() =
=![]() ≥4,
≥4,
当m=0时,即Q(0,﹣1)时,△QDE的面积S取得最小值4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
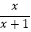 ,x∈[2,4].
,x∈[2,4].
(1)判断f(x)的单调性,并利用单调性的定义证明:
(2)求f(x)在[2,4]上的最值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xsinx,有下列四个结论: ①函数f(x)的图象关于y轴对称;
②存在常数T>0,对任意的实数x,恒有f(x+T)=f(x);
③对于任意给定的正数M,都存在实数x0 , 使得|f(x0)|≥M;
④函数f(x)在[0,π]上的最大值是 .
.
其中正确结论的序号是(请把所有正确结论的序号都填上). -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数

(1)求
 的单调区间;
的单调区间;(2)若
 为整数,且当
为整数,且当 时,
时,  恒成立,其中
恒成立,其中 为
为 的导函数,求
的导函数,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某中学高三文科班学生共有
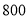 人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取
人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取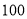 人进行成绩抽样统计,先将
人进行成绩抽样统计,先将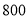 人按
人按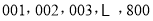 进行编号.
进行编号.(Ⅰ)如果从第
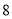 行第
行第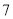 列的数开始向右读,请你依次写出最先检测的
列的数开始向右读,请你依次写出最先检测的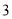 个人的编号;(下面摘取了第
个人的编号;(下面摘取了第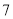 行 至第
行 至第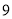 行)
行)
(Ⅱ)抽的
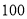 人的数学与地理的水平测试成绩如下表:
人的数学与地理的水平测试成绩如下表:人数
数学
优秀
良好
及格
地
理
优秀
7
20
5
良好
9
18
6
及格
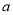
4
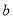
成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有
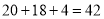 人,若在该样本中,数学成绩优秀率为
人,若在该样本中,数学成绩优秀率为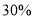 ,求
,求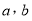 的值.
的值.(Ⅲ)将
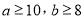 的
的 表示成有序数对
表示成有序数对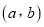 ,求“在地理成绩为及格的学生中,数学成绩为优秀的人数比及格的人数少”的数对
,求“在地理成绩为及格的学生中,数学成绩为优秀的人数比及格的人数少”的数对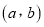 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
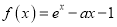 (
(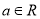 )(
)(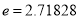 …是自然对数的底数).
…是自然对数的底数).(1)求
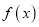 单调区间;
单调区间;(2)讨论
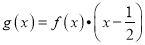 在区间
在区间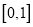 内零点的个数.
内零点的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】设y1=loga(3x+1),y2=loga(﹣3x),其中a>0且a≠1.
(1)若y1=y2 , 求x的值;
(2)若y1>y2 , 求x的取值范围.
相关试题

