【题目】已知函数![]() 有两个不同的零点.
有两个不同的零点.
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)记两个零点分别为![]() ,且
,且![]() ,已知
,已知![]() ,若不等式
,若不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(I)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)方程![]() 在
在![]() 有两个不同跟等价于函数
有两个不同跟等价于函数![]() 与函数
与函数![]() 的图像在
的图像在![]() 上有两个不同交点,对
上有两个不同交点,对![]() 进行求导,通过单调性画出
进行求导,通过单调性画出![]() 的草图,由
的草图,由![]() 与
与![]() 有两个交点进而得出
有两个交点进而得出![]() 的取值范围; (Ⅱ)分离参数得:
的取值范围; (Ⅱ)分离参数得:![]() ,从而可得
,从而可得![]() 恒成立;再令
恒成立;再令![]() ,从而可得不等式
,从而可得不等式![]() 在
在![]() 上恒成立,再令
上恒成立,再令![]() ,从而利用导数化恒成立问题为最值问题即可.
,从而利用导数化恒成立问题为最值问题即可.
试题解析:(I)依题意,函数![]() 的定义域为
的定义域为![]() ,
,
所以方程![]() 在
在![]() 有两个不同跟等价于函数
有两个不同跟等价于函数![]() 与函数
与函数![]() 的图像在
的图像在![]() 上有两个不同交点.
上有两个不同交点.
又![]() ,即当
,即当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
从而![]() .
.
又![]() 有且只有一个零点是1,且在
有且只有一个零点是1,且在![]() 时,
时,![]() ,在
,在![]() 时,
时,![]() ,
,
所以![]() 的草图如下:
的草图如下:
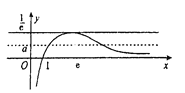
可见,要想函数![]() 与函数
与函数![]() 在图像
在图像![]() 上有两个不同交点,只需
上有两个不同交点,只需![]() .
.
(Ⅱ)由(I)可知![]() 分别为方程
分别为方程![]() 的两个根,即
的两个根,即![]() ,
,![]() ,
,
所以原式等价于![]() .
.
因为![]() ,
,![]() ,所以原式等价于
,所以原式等价于![]() .
.
又由![]() ,
,![]() 作差得,
作差得,![]() ,即
,即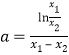 .
.
所以原式等价于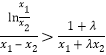 .
.
因为![]() ,原式恒成立,即
,原式恒成立,即![]() 恒成立.
恒成立.
令![]() ,则不等式
,则不等式![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,则
,则![]() ,
,
当![]() 时,可见
时,可见![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增,又
上单调递增,又![]() 在
在![]() 恒成立,符合题意;
恒成立,符合题意;
当![]() 时,可见当
时,可见当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 时单调递增,在
时单调递增,在![]() 时单调递减.
时单调递减.
又![]() ,所以
,所以![]() 在
在![]() 上不能恒小于0,不符合题意,舍去.
上不能恒小于0,不符合题意,舍去.
综上所述,若不等式![]() 恒成立,只须
恒成立,只须![]() ,又
,又![]() ,所以
,所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}
(1)若a=-2,求B∩A,B∩UA;
(2)若BA,求实数a取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正三棱柱
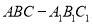 中,
中,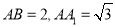 ,点
,点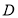 为
为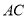 的中点,点
的中点,点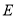 在线段
在线段 上.
上.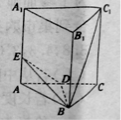
(Ⅰ)当
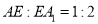 时,求证
时,求证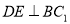 ;
;(Ⅱ)是否存在点
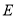 ,使二面角
,使二面角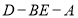 等于60°?若存在,求
等于60°?若存在,求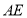 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B、C是△ABC的三个内角,向量m=(-1,
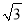 ),n=(cosA,sinA),且m·n=1.
),n=(cosA,sinA),且m·n=1.(1)求角A;
(2)若
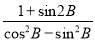 =-3,求tanC.
=-3,求tanC. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 .
.(1)求f(x)的定义域及最小正周期;
(2)求f(x)的单调递增区间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
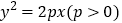 ,过点
,过点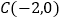 的直线
的直线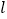 交抛物线于
交抛物线于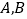 两点,坐标原点为
两点,坐标原点为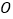 ,且
,且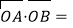 12.
12.(Ⅰ)求抛物线的方程;
(Ⅱ)当以
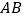 为直径的圆的面积为
为直径的圆的面积为 时,求
时,求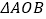 的面积
的面积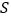 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了参加师大附中第30界田径运动会的开幕式,高三年级某6个班联合到集市购买了6根竹竿,作为班旗的旗杆之用,它们的长度分别为3.8,4.3,3.6,4.5,4.0,4.1(单位:米).
(Ⅰ)若从中随机抽取两根竹竿,求长度之差不超过0.5米的概率;
(Ⅱ)若长度不小于4米的竹竿价格为每根10元,长度小于4米的竹竿价格为每根
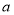 元.从这6根竹竿中随机抽取两根,若期望这两根竹竿的价格之和为18元,求
元.从这6根竹竿中随机抽取两根,若期望这两根竹竿的价格之和为18元,求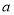 的值.
的值.
相关试题

