【题目】为了参加师大附中第30界田径运动会的开幕式,高三年级某6个班联合到集市购买了6根竹竿,作为班旗的旗杆之用,它们的长度分别为3.8,4.3,3.6,4.5,4.0,4.1(单位:米).
(Ⅰ)若从中随机抽取两根竹竿,求长度之差不超过0.5米的概率;
(Ⅱ)若长度不小于4米的竹竿价格为每根10元,长度小于4米的竹竿价格为每根![]() 元.从这6根竹竿中随机抽取两根,若期望这两根竹竿的价格之和为18元,求
元.从这6根竹竿中随机抽取两根,若期望这两根竹竿的价格之和为18元,求![]() 的值.
的值.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
试题分析: (Ⅰ)因为![]() 根竹竿长度之差超过
根竹竿长度之差超过![]() 米的两根竹竿长可能是
米的两根竹竿长可能是![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() .
.
先求对立事件的概率![]()
![]() 所求概率
所求概率![]() ;(Ⅱ)设任取两根竹竿的价格之和为
;(Ⅱ)设任取两根竹竿的价格之和为![]()
![]()
![]() 的可能取值
的可能取值![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
试题解析:(Ⅰ)因为![]() 根竹竿的长度从小到大依次为
根竹竿的长度从小到大依次为![]() ,其中长度之差超过
,其中长度之差超过![]() 米的两根竹竿长可能是
米的两根竹竿长可能是![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() .
.
设“抽取两根竹竿的长度之差不超过![]() 米”为事件
米”为事件![]() ,则
,则
![]() ,所以
,所以![]() .
.
故所求的概率为![]() .
.
(Ⅱ)设任取两根竹竿的价格之和为![]() ,则
,则![]() 的可能取值为
的可能取值为![]() .
.
其中![]() .
.
所以![]() .
.
令![]() ,得
,得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
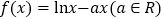 有两个不同的零点.
有两个不同的零点.(Ⅰ)求
 的取值范围;
的取值范围;(Ⅱ)记两个零点分别为
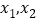 ,且
,且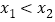 ,已知
,已知 ,若不等式
,若不等式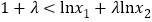 恒成立,求
恒成立,求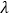 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 .
.(1)求f(x)的定义域及最小正周期;
(2)求f(x)的单调递增区间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
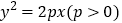 ,过点
,过点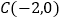 的直线
的直线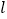 交抛物线于
交抛物线于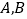 两点,坐标原点为
两点,坐标原点为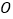 ,且
,且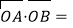 12.
12.(Ⅰ)求抛物线的方程;
(Ⅱ)当以
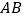 为直径的圆的面积为
为直径的圆的面积为 时,求
时,求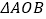 的面积
的面积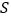 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
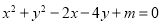 .(14分)
.(14分)(1)此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M、N两点,且
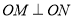 (O为坐标原点),求m的值;
(O为坐标原点),求m的值;(3)在(2)的条件下,求以
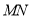 为直径的圆的方程.
为直径的圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家商场对同一种商品展开促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示转盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为
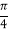 ,边界忽略不计)即为中奖.
,边界忽略不计)即为中奖.乙商场:从装有4个白球,4个红球和4个篮球的盒子中一次性摸出3球(这些球初颜色外完全相同),如果摸到的是3个不同颜色的球,即为中奖.

(Ⅰ)试问:购买该商品的顾客在哪家商场中奖的可能性大?说明理由;
(Ⅱ)记在乙商场购买该商品的顾客摸到篮球的个数为
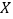 ,求
,求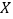 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
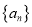 的前
的前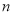 项和为
项和为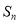 ,且满足
,且满足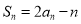 ,求数列
,求数列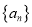 的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.
的通项公式.勤于思考的小红设计了下面两种解题思路,请你选择其中一种并将其补充完整.思路1:先设
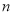 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出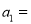 _________,
_________, 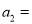 __________,
__________, 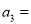 _________.
_________.猜想:
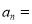 _______.
_______.然后用数学归纳法证明.证明过程如下:
①当
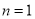 时,________________,猜想成立
时,________________,猜想成立②假设
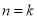 (
(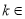 N*)时,猜想成立,即
N*)时,猜想成立,即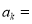 _______.
_______.那么,当
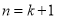 时,由已知
时,由已知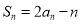 ,得
,得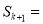 _________.
_________.又
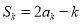 ,两式相减并化简,得
,两式相减并化简,得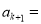 _____________(用含
_____________(用含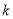 的代数式表示).
的代数式表示).所以,当
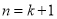 时,猜想也成立.
时,猜想也成立.根据①和②,可知猜想对任何
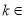 N*都成立.
N*都成立.思路2:先设
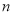 的值为1,根据已知条件,计算出
的值为1,根据已知条件,计算出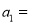 _____________.
_____________.由已知
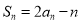 ,写出
,写出 与
与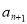 的关系式:
的关系式: 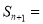 _____________________,
_____________________,两式相减,得
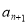 与
与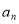 的递推关系式:
的递推关系式: 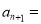 ____________________.
____________________.整理:
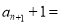 ____________.
____________.发现:数列
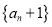 是首项为________,公比为_______的等比数列.
是首项为________,公比为_______的等比数列.得出:数列
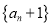 的通项公式
的通项公式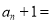 ____,进而得到
____,进而得到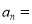 ____________.
____________.
相关试题

