【题目】已知A、B、C是△ABC的三个内角,向量m=(-1, ![]() ),n=(cosA,sinA),且m·n=1.
),n=(cosA,sinA),且m·n=1.
(1)求角A;
(2)若![]() =-3,求tanC.
=-3,求tanC.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)由m·n=1,代入坐标用两角和与差的正弦公式化简,即可求出角A;(2)将已知条件用完全平方公式和平方差公式化简,可得![]() =-3,分式上下同除以
=-3,分式上下同除以![]() ,解出
,解出![]() ,又tanC=tan[π-(A+B)],利用诱导公式和两角和与差的正切公式化简,把
,又tanC=tan[π-(A+B)],利用诱导公式和两角和与差的正切公式化简,把![]() 和
和![]() 的值代入即可.
的值代入即可.
试题解析:
(1)∵m·n=1,
∴![]() sinA-cosA=1,2(sinA·
sinA-cosA=1,2(sinA·![]() -cosA·
-cosA·![]() )=1,
)=1,
sin(A-![]() )=
)=![]() ,
,
∵0<A<π,- ![]() <A-
<A-![]() <
<![]() ,
,
∴A-![]() =
=![]() .∴A=
.∴A=![]() .
.
(2)由题知![]() =-3,
=-3,
∴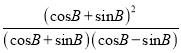 =-3
=-3
∴![]() =-3
=-3
∴![]() =-3,∴tanB=2.
=-3,∴tanB=2.
∴tanC=tan[π-(A+B)]
=-tan(A+B)=-![]() =
=![]() .
.
点睛:本题考查平面向量数量积的坐标运算,同角三角函数的基本关系和两角和与差的正切公式. 平面向量的数量积计算问题,往往有两种形式,一是利用数量积的定义式,二是利用数量积的坐标运算公式,涉及几何图形的问题,先建立适当的平面直角坐标系,可起到化繁为简的妙用. 利用向量夹角公式、模公式及向量垂直的充要条件,可将有关角度问题、线段长问题及垂直问题转化为向量的数量积来解决.列出方程组求解未知数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在寒假社会实践活动中,对白天平均气温与某家奶茶店的
 品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温
品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温 (
( )与该奶茶店的
)与该奶茶店的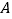 品牌饮料销量
品牌饮料销量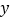 (杯),得到如表数据:
(杯),得到如表数据:日期
1月11号
1月12号
1月13号
1月14号
1月15号
平均气温
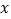 (
(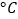 )
)9
10
12
11
8
销量
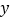 (杯)
(杯)23
25
30
26
21
(1)若先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出
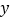 关于
关于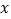 的线性回归方程式
的线性回归方程式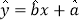 ;
;(3)根据(2)所得的线性回归方程,若天气预报1月16号的白天平均气温为
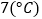 ,请预测该奶茶店这种饮料的销量.
,请预测该奶茶店这种饮料的销量.(参考公式:
 ,
,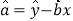 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】设全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}
(1)若a=-2,求B∩A,B∩UA;
(2)若BA,求实数a取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正三棱柱
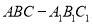 中,
中,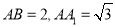 ,点
,点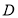 为
为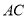 的中点,点
的中点,点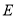 在线段
在线段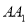 上.
上.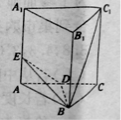
(Ⅰ)当
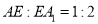 时,求证
时,求证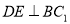 ;
;(Ⅱ)是否存在点
 ,使二面角
,使二面角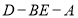 等于60°?若存在,求
等于60°?若存在,求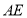 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
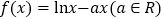 有两个不同的零点.
有两个不同的零点.(Ⅰ)求
 的取值范围;
的取值范围;(Ⅱ)记两个零点分别为
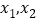 ,且
,且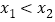 ,已知
,已知 ,若不等式
,若不等式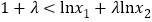 恒成立,求
恒成立,求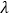 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 .
.(1)求f(x)的定义域及最小正周期;
(2)求f(x)的单调递增区间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
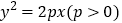 ,过点
,过点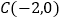 的直线
的直线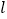 交抛物线于
交抛物线于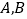 两点,坐标原点为
两点,坐标原点为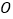 ,且
,且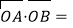 12.
12.(Ⅰ)求抛物线的方程;
(Ⅱ)当以
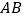 为直径的圆的面积为
为直径的圆的面积为 时,求
时,求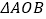 的面积
的面积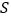 的值.
的值.
相关试题

