【题目】已知表1是某年部分日期的天安门广场升旗时刻表.
表1:某年部分日期的天安门广场升旗时刻表

将表1中的升旗时刻化为分数后作为样本数据(如:![]() 可化为
可化为![]() ).
).
(Ⅰ)请补充完成下面的频率分布表及频率分布直方图;
|
|
(Ⅱ)若甲学校从上表日期中随机选择一天观看升旗.试估计甲学校观看升旗的时刻早于6:00的概率;
(Ⅲ)若甲,乙两个学校各自从表1中五月、六月的日期中随机选择一天观看升旗, 求两校观看升旗的时刻均不早于5:00的概率.
参考答案:
【答案】(Ⅰ)详见解析;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)由天安门广场升旗时刻表即可得到频率分布表及频率分布直方图;
(Ⅱ)利用古典概型概率公式可得结果;
(Ⅲ)利用古典概型概率公式可得结果.
解:(Ⅰ)频率分布表及频率分布直方图如下:

分组 | 频数 | 频率 |
4:00—4:59 | 3 | 0.15 |
5:00—5:59 | 5 | 0.25 |
6:00—6:59 | 7 | 0.35 |
7:00—7:59 | 5 | 0.25 |
合计 | 20 | 1 |
(II) 由表知,甲学校从上表20次日期中随机选择一天观看升旗,观看升旗的时刻早于6:00的日期为8次,所以,估计甲学校观看升旗的时刻早于6:00的概率为![]() .
.
(III) 由表知,五月、六月的日期中不早于5:00的时间为2次,共5次.
设按表1中五月、六月的日期先后顺序,甲选择一天观看升旗分别为![]() ,乙选择一天观看升旗分别为
,乙选择一天观看升旗分别为![]() ,
,
则甲,乙两个学校观看升旗的时刻的基本事件空间![]() 为:
为:![]()
![]()
![]()
![]()
![]() 其中基本事件为25个.
其中基本事件为25个.
设两校观看升旗的时刻均不早于5:00为事件![]() ,包含基本事件为:
,包含基本事件为:
![]() ,共4个,
,共4个,
所以![]() ,即两校观看升旗的时刻均不早于5:00的概率为
,即两校观看升旗的时刻均不早于5:00的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE=
 ,∠EAD=∠EAB.
,∠EAD=∠EAB. 
(1)证明:平面ACEF⊥平面ABCD;
(2)若AE与平面ABCD所成角为60°,求二面角B﹣EF﹣D的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司制造两种电子设备:影片播放器和音乐播放器.在每天生产结束后,要对产品进行检测,故障的播放器会被移除进行修复. 下表显示各播放器每天制造的平均数量以及平均故障率.
商品类型
播放器每天平均产量
播放器每天平均故障率
影片播放器
3000
4%
音乐播放器
9000
3%
下面是关于公司每天生产量的叙述:
①每天生产的播放器有三分之一是影片播放器;
②在任何一批数量为100的影片播放器中,恰好有4个会是故障的;
③如果从每天生产的音乐播放器中随机选取一个进行检测,此产品需要进行修复的概率是0.03.
上面叙述正确的是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
空气质量指数
(0,50]
(50,100]
(100,150]
(150,200]
(200,250]
(250,300]
空气质量等级
1级优
2级良
3级轻度污染
4级中度污染
5级重度污染
6级严重污染
该社团将该校区在2016年100天的空气质量指数监测数据作为样本,绘制的频率分布直方图如图,把该直方图所得频率估计为概率.

(Ⅰ)请估算2017年(以365天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)该校2017年6月7、8、9日将作为高考考场,若这三天中某天出现5级重度污染,需要净化空气费用10000元,出现6级严重污染,需要净化空气费用20000元,记这三天净化空气总费用为X元,求X的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列两个命题:
 函数
函数 在[2,+∞)单调递增;
在[2,+∞)单调递增;  关于
关于 的不等式
的不等式 的解集为
的解集为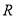 .若
.若 为真命题,
为真命题,  为假命题,求
为假命题,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 的圆心在
的圆心在 轴上,且经过点
轴上,且经过点 ,
, .
.(Ⅰ)求线段AB的垂直平分线方程;
(Ⅱ)求圆
 的标准方程;
的标准方程;(Ⅲ)过点
 的直线
的直线 与圆
与圆 相交于
相交于 、
、 两点,且
两点,且 ,求直线
,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
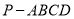 中,PA⊥平面ABCD,CD⊥AD,BC∥AD,
中,PA⊥平面ABCD,CD⊥AD,BC∥AD, .
.
(Ⅰ)求证:CD⊥PD;
(Ⅱ)求证:BD⊥平面PAB;
(Ⅲ)在棱PD上是否存在点M,使CM∥平面PAB,若存在,确定点M的位置,若不存在,请说明理由.
相关试题


