【题目】设a为实数,函数![]() ,x∈R.
,x∈R.
(I)当a=0时,求f(x)在区间[0,2]上的最大值和最小值;
(Ⅱ)求函数f(x)的最小值.
参考答案:
【答案】(I)见解析;(II)当![]() 时,
时, ![]() 的最小值为
的最小值为![]() ;当
;当![]() 时,
时, ![]() 的最小值为
的最小值为![]()
【解析】试题分析:(Ⅰ)根据![]() 时,
时, ![]() 在
在![]() 上,取绝对值,根据二次函数的单调性即可求解在区间
上,取绝对值,根据二次函数的单调性即可求解在区间![]() 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)利用零点分段去绝对值,根据对称轴分情况讨论即可求函数![]() 的最小值
的最小值
试题解析:(I)当![]() ,
, ![]() 时,函数
时,函数![]() ,
,
因为![]() 的图象抛物线开口向上,对称轴为
的图象抛物线开口向上,对称轴为![]() ,
,
所以,当![]() 时,
时, ![]() 值最小,最小值为
值最小,最小值为![]() ;
;
当![]() 时,
时, ![]() 值最大,最大值为3.
值最大,最大值为3.
(II)①当![]() 时,函数
时,函数![]() .
.
若![]() ,则
,则![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上的最小值为
上的最小值为![]() ;
;
若![]() ,则函数
,则函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ;
;
②当![]() 时,
时, ![]() .
.
若![]() ,则
,则![]() 在
在![]() 上的最小值为
上的最小值为![]() ;
;
若![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增, ![]() .
.
所以,当![]() 时,
时, ![]() ,
, ![]() 的最小值为
的最小值为![]() .
.
当![]() 时,
时, ![]() ,
, ![]() 的最小值为
的最小值为![]() .
.
当![]() 时,
时, ![]() 的最小值为
的最小值为![]() 与
与![]() 中小者.所以,当
中小者.所以,当![]() 时,
时, ![]() 的最小值为
的最小值为![]() ;当
;当![]() 时,
时, ![]() 的最小值为
的最小值为![]() .
.
综上,当![]() 时,
时, ![]() 的最小值为
的最小值为![]() ;当
;当![]() 时,
时, ![]() 的最小值为
的最小值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直三棱柱ABC﹣A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB的中点,AC=BC=2,AA1=4.

(1)当E是棱CC1的中点时,求证:CF∥平面AEB1;
(2)在棱CC1上是否存在点E,使得二面角A﹣EB1﹣B的大小是45°?若存在,求出CE的长,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB⊥BC,AB=
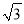 BC=
BC=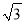 a,a∈[1,3],圆A是以A为圆心、半径为2的圆,圆B是以B为圆心、半径为1的圆,设点E、F分别为圆A、圆B上的动点,
a,a∈[1,3],圆A是以A为圆心、半径为2的圆,圆B是以B为圆心、半径为1的圆,设点E、F分别为圆A、圆B上的动点, 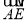 ∥
∥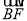 (且
(且 与
与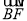 同向),设∠BAE=θ(θ∈[0,π]).
同向),设∠BAE=θ(θ∈[0,π]).(I)当a=
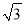 ,且θ=
,且θ=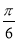 时,求
时,求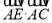 的值;
的值;(Ⅱ)用a,θ表示出
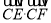 ,并给出一组a,θ的值,使得
,并给出一组a,θ的值,使得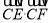 最小.
最小.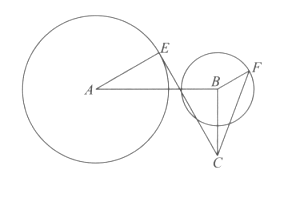
-
科目: 来源: 题型:
查看答案和解析>>【题目】衡州市临枣中学高二某小组随机调查芙蓉社区160个人,以研究这一社区居民在20:00﹣22:00时间段的休闲方式与性别的关系,得到下面的数据表:
休闲方式
性别看电视
看书
合计
男
20
100
120
女
20
20
40
合计
40
120
160
下面临界值表:
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.072
2.706
3.841
5.024
6.635
7.879
10.828
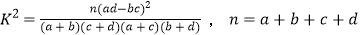
(Ⅰ)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X,求X的分别列和期望;
(Ⅱ)根据以上数据,能否有99%的把握认为“在20:00﹣22:00时间段的休闲方式与性别有关系”? -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)满足:对于s,t∈[0,+∞),都有f(s)≥0,f(t)≥0,且f(s)+f(t)≤f(s+t),则称函数f (x)为“T函数”.
(I)试判断函数f1(x)=x2与f2(x)=lg(x+1)是否是“T函数”,并说明理由;
(Ⅱ)设f (x)为“T函数”,且存在x0∈[0,+∞),使f(f(x0))=x0.求证:f (x0) =x0;
(Ⅲ)试写出一个“T函数”f(x),满足f(1)=1,且使集合{y|y=f(x),0≤x≤1)中元素的个数最少.(只需写出结论)
-
科目: 来源: 题型:
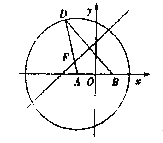
查看答案和解析>>【题目】如图,在平面直角坐标系
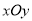 中,圆
中,圆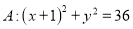 ,点
,点 ,点
,点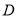 是圆
是圆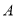 上的动点,线段
上的动点,线段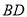 的垂直平分线交线段
的垂直平分线交线段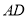 于点
于点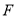 ,设
,设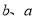 分别为点
分别为点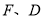 的横坐标,定义函数
的横坐标,定义函数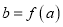 ,给出下列结论:
,给出下列结论:①
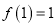 ;②
;②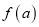 是偶函数;③
是偶函数;③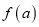 在定义域上是增函数;
在定义域上是增函数;④
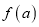 图象的两个端点关于圆心
图象的两个端点关于圆心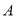 对称;
对称;⑤动点
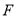 到两定点
到两定点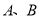 的距离和是定值.
的距离和是定值.其中正确的是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
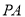 是圆柱的母线,
是圆柱的母线, 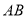 是圆柱底面圆的直径,
是圆柱底面圆的直径, 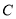 是底面圆周上异于
是底面圆周上异于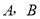 的任意一点,
的任意一点, 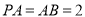 .
.(1)求证:
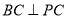 ;
;(2)求三棱锥
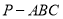 体积的最大值,并写出此时三棱锥
体积的最大值,并写出此时三棱锥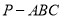 外接球的表面积.
外接球的表面积.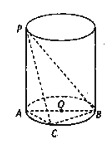
相关试题

