【题目】某校为了解高一新生对文理科的选择,对1 000名高一新生发放文理科选择调查表,统计知,有600名学生选择理科,400名学生选择文科.分别从选择理科和文科的学生随机各抽取20名学生的数学成绩得如下累计表:
分数段 | 理科人数 | 文科人数 |
|
| |
|
| |
|
|
|
| 正 | 正 |
| 正 |
|
|
|
|
(1)从统计表分析,比较选择文理科学生的数学平均分及学生选择文理科的情况,并绘制理科数学成绩的频率分布直方图.

(2)根据你绘制的频率分布直方图,估计意向选择理科的学生的数学成绩的中位数与平均分.
参考答案:
【答案】(1)详见解析;(2)中位数80,平均分79.5.
【解析】
根据表格对应算出频率/组距的相关数据,从而绘制频率分布直方图;
根据中位数和平均数的相关定义建立等式即可算出.
解:(1)从统计表看出选择理科的学生的数学平均成绩高于选择文科的学生的数学平均成绩,反映了数学成绩对学生选择文理科有一定的影响,频率分布直方图如下
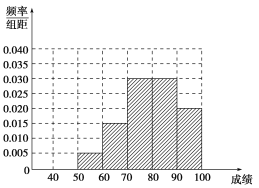
(2)从频率分布直方图知,数学成绩有![]() 小于或等于80分,
小于或等于80分,![]() 大于或等于80分,所以中位数为80分.
大于或等于80分,所以中位数为80分.
平均分为![]() ,
,
即估计选择理科的学生的平均分为79.5分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时, .
.(1)求
 及
及 的值;
的值;(2)求函数
 在
在 上的解析式;
上的解析式;(3)若关于
 的方程
的方程 有四个不同的实数解,求实数
有四个不同的实数解,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]
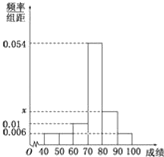
(Ⅰ)求图中
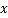 的值,并估计该班期中考试数学成绩的众数;
的值,并估计该班期中考试数学成绩的众数;(Ⅱ)从成绩不低于90分的学生和成绩低于50分的学生中随机选取2人,求这2人成绩均不低于90分的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地某路无人驾驶公交车发车时间间隔
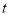 (单位:分钟)满足
(单位:分钟)满足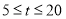 ,
,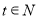 .经测算,该路无人驾驶公交车载客量
.经测算,该路无人驾驶公交车载客量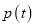 与发车时间间隔
与发车时间间隔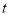 满足:
满足: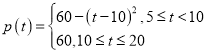 ,其中
,其中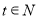 .
.(1)求
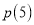 ,并说明
,并说明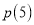 的实际意义;
的实际意义;(2)若该路公交车每分钟的净收益
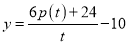 (元),问当发车时间间隔为多少时,该路公交车每分钟的净收益最大?并求每分钟的最大净收益.
(元),问当发车时间间隔为多少时,该路公交车每分钟的净收益最大?并求每分钟的最大净收益. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两支篮球队赛季总决赛采用7场4胜制,每场必须分出胜负,场与场之间互不影响,只要有一队获胜4场就结束比赛.现已比赛了4场,且甲篮球队胜3场.已知甲球队第5,6场获胜的概率均为
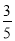 ,但由于体力原因,第7场获胜的概率为
,但由于体力原因,第7场获胜的概率为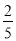 .
.(1)求甲队分别以
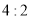 ,
,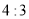 获胜的概率;
获胜的概率;(2)设
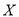 表示决出冠军时比赛的场数,求
表示决出冠军时比赛的场数,求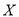 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知参加某项活动的六名成员排成一排合影留念,且甲乙两人均在丙领导人的同侧,则不同的排法共有( )
A. 240种 B. 360种 C. 480种 D. 600种
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为椭圆
为椭圆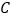 的左、右顶点,
的左、右顶点,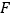 为其右焦点,
为其右焦点,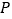 是椭圆
是椭圆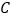 上异于
上异于 的动点,且
的动点,且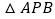 面积的最大值为
面积的最大值为 .
.(1)求椭圆
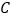 的方程;
的方程;(2)直线
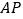 与椭圆在点
与椭圆在点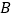 处的切线交于点
处的切线交于点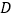 ,当点
,当点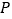 在椭圆上运动时,求证:以
在椭圆上运动时,求证:以  为直径的圆与直线
为直径的圆与直线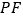 恒相切.
恒相切.
相关试题

