【题目】已知函数![]() (
(![]() )在
)在![]() 处取得极值.
处取得极值.
(1)求![]() 的单调区间;
的单调区间;
(2)讨论![]() 的零点个数,并说明理由.
的零点个数,并说明理由.
参考答案:
【答案】(1)单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(2)见解析
;(2)见解析
【解析】分析:(1)由题意可得![]() , 则
, 则![]() .据此可知
.据此可知![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)由(1)知![]() 在
在![]() 处取得最大值
处取得最大值![]() . 分类讨论有:①当
. 分类讨论有:①当![]() 时,
时,![]() 无零点. ②当
无零点. ②当![]() 时,
时,![]() 有一个零点. ③当
有一个零点. ③当![]() 时,
时,![]() 有两个零点.
有两个零点.
详解:(1)因为![]() ,
,
又![]() ,即
,即![]() ,解得
,解得![]() .
.
令![]() ,即
,即![]() ,解得
,解得![]() ;
;
令![]() ,即
,即![]() ,解得
,解得![]() .
.
所以![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)由(1)知![]() 在
在![]() 处取得最大值
处取得最大值![]() .
.
①当![]() 即
即![]() 时,
时,![]() ,所以
,所以![]() 无零点.
无零点.
②当![]() 即
即![]() 时,当且仅当
时,当且仅当![]() 时,
时,![]() ,
,
所以![]() 有一个零点.
有一个零点.
③当![]() 即
即![]() 时,
时,![]() ,
,
因为![]() ,且
,且![]() ,
,
又![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 在
在![]() 上有且只有一个零点.
上有且只有一个零点.
因为![]() ,且
,且![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,所以
,所以![]() .
.
又![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() 在上
在上![]() 有且只有一个零点.
有且只有一个零点.
故当![]() 时,
时,![]() 有两个零点.
有两个零点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 :
: (
( 为参数),曲线
为参数),曲线 :
: (
( 为参数).
为参数).(1)设
 与
与 相交于
相交于 ,
, 两点,求
两点,求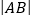 的值;
的值;(2)若把曲线
 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的 ,纵坐标压缩为原来的
,纵坐标压缩为原来的 ,得到曲线
,得到曲线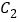 ,设点
,设点 是曲线
是曲线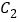 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在直角坐标系
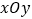 中,曲线
中,曲线 的方程是
的方程是 ,直线
,直线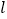 经过点
经过点 ,倾斜角为
,倾斜角为 ,以
,以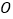 为极点,
为极点, 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.(1)写出曲线
 的极坐标方程和直线
的极坐标方程和直线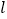 的参数方程;
的参数方程;(2)设直线
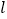 与曲线
与曲线 相交于
相交于 ,
,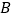 两点,求
两点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“双十一网购狂欢节”源于淘宝商城(天猫)2009年11月11 日举办的促销活动,当时参与的商家数量和促销力度均有限,但营业额远超预想的效果,于是11月11日成为天猫举办大规模促销活动的固定日期.如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商分析近8年“双十一”期间的宣传费用
 (单位:万元)和利润
(单位:万元)和利润 (单位:十万元)之间的关系,得到下列数据:
(单位:十万元)之间的关系,得到下列数据:
2
3
4
5
6
8
9
11

1
2
3
3
4
5
6
8
(1)请用相关系数
 说明
说明 与
与 之间是否存在线性相关关系(当
之间是否存在线性相关关系(当 时,说明
时,说明 与
与 之间具有线性相关关系);
之间具有线性相关关系);(2)根据(1)的判断结果,建立
 与
与 之间的回归方程,并预测当
之间的回归方程,并预测当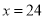 时,对应的利润
时,对应的利润 为多少(
为多少( 精确到0.1).
精确到0.1).附参考公式:回归方程中
 中
中 和
和 最小二乘估计分别为
最小二乘估计分别为 ,相关系数
,相关系数
参考数据:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在极坐标系中,曲线
 :
: ,曲线
,曲线 :
: .以极点为坐标原点,极轴为
.以极点为坐标原点,极轴为 轴正半轴建立直角坐标系
轴正半轴建立直角坐标系 ,曲线
,曲线 的参数方程为
的参数方程为 (
(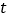 为参数).
为参数).(1)求
 ,
, 的直角坐标方程;
的直角坐标方程;(2)
 与
与 ,
, 交于不同四点,这四点在
交于不同四点,这四点在 上的排列顺次为
上的排列顺次为 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的几何体中,四边形
 是等腰梯形,
是等腰梯形, ∥
∥ ,
, 平面
平面 .
.(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】记
 表示大于
表示大于 的整数
的整数 的十位数,例如
的十位数,例如 ,
, .已知
.已知 ,
, ,
, 都是大于
都是大于 的互不相等的整数,现有如下
的互不相等的整数,现有如下 个命题:
个命题:①若
 ,则
,则 ;②
;② ,
, 且
且 ;
;③若
 是质数,则
是质数,则 也是质数;④若
也是质数;④若 ,
, ,
, 成等差数列,则
成等差数列,则 ,
, ,
, 可能成等比数列.
可能成等比数列.其中所有的真命题为( )
A. ② B. ③④ C. ①②④ D. ①②③④
相关试题

