【题目】质检过后,某校为了解科班学生的数学、物理学习情况,利用随机数表法从全年极![]() 名理科生抽取
名理科生抽取![]() 名学生的成绩进行统计分析.已知学生考号的后三位分别为
名学生的成绩进行统计分析.已知学生考号的后三位分别为![]() .
.
(Ⅰ)若从随机数表的第![]() 行第
行第![]() 列的数开始向右读,请依次写出抽取的前
列的数开始向右读,请依次写出抽取的前![]() 人的后三位考号;
人的后三位考号;
(Ⅱ)如果题(Ⅰ)中随机抽取到的![]() 名同学的数学、物理成绩(单位:分)对应如下表:
名同学的数学、物理成绩(单位:分)对应如下表:
数学成绩 | 87 | 91 | 90 | 89 | 93 |
物理成绩 | 89 | 90 | 91 | 88 | 92 |
求这两科成绩的平均数和方差,并且分析哪科成绩更稳定。
附:(下面是摘自随机数表的第![]() 行到第6行)
行到第6行)
………





………
参考答案:
【答案】(1) ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;(2) 物理成绩更稳定
;(2) 物理成绩更稳定
【解析】分析:(1) 随机数表抽取方法,先依次取三个数字,若不在编号中或前面已取则舍去,继续取下一个三个数字,直至取完,(2)根据平均数公式以及方差公式分别求平均数与方差,在平均值一样情况下,方差越小越稳定.
详解:
(1)抽取的前![]() 人的后三位考号分别为:
人的后三位考号分别为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)由题中数据可得![]() ,
,![]()
∴![]()
![]()
由![]() ,可知物理成绩更稳定.
,可知物理成绩更稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是( )
A. 若两条直线和同一个平面所成的角相等,则这两条直线平行
B. 若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行
C. 若两个平面都垂直于第三个平面,则这两个平面平行
D. 若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 中,
中, ,
, ,
, ,
, ,
, ,
, 分别在
分别在 ,
, 上,
上, ,现将四边形
,现将四边形 沿
沿 折起,使平面
折起,使平面 平面
平面 .
.(Ⅰ)若
 ,在折叠后的线段
,在折叠后的线段 上是否存在一点
上是否存在一点 ,且
,且 ,使得
,使得 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由;
的值;若不存在,说明理由;(Ⅱ)求三棱锥
 的体积的最大值.
的体积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占
 .现从参与关注生态文明建设的人群中随机选出
.现从参与关注生态文明建设的人群中随机选出 人,并将这
人,并将这 人按年龄分组:第
人按年龄分组:第 组
组 ,第
,第 组
组 ,第
,第 组
组 ,第
,第 组
组 ,第
,第 组
组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(Ⅰ)求出
 的值;
的值;(Ⅱ)求出这
 人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);(Ⅲ)现在要从年龄较小的第
 、
、 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取 人,则第
人,则第 、
、 组分别抽取多少人?
组分别抽取多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
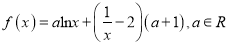 .
.(Ⅰ)试求函数
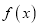 的单调区间;
的单调区间;(Ⅱ)若不等式
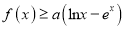 对任意的
对任意的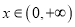 恒成立,求实数
恒成立,求实数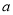 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】有9本不同的课外书,分给甲、乙、丙三名同学,求在下列条件下,各有多少种分法?
(1)甲得4本,乙得3本,丙得2本;
(2)一人得4本,一人得3本,一人得2本;
(3)甲、乙、丙各得3本.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次足球比赛共12支球队参加,分三个阶段进行.
(1)小组赛:经抽签分成甲、乙两组,每组6队进行单循环比赛,以积分及净剩球数取前两名;
(2)半决赛:甲组第一名与乙组第二名,乙组第一名与甲组第二名作主客场交叉淘汰赛(每两队主客场各赛一场)决出胜者;
(3)决赛:两个胜队参加决赛一场,决出胜负.
问全程赛程共需比赛多少场?
相关试题

