【题目】已知双曲线过点(3,-2)且与椭圆4x2+9y2=36有相同的焦点.
(I)求双曲线的标准方程.
(II)若点M在双曲线上, ![]() 是双曲线的左、右焦点,且|MF1|+|MF2|=
是双曲线的左、右焦点,且|MF1|+|MF2|=![]() 试判断
试判断![]() 的形状.
的形状.
参考答案:
【答案】(1) ![]() (2)
(2) ![]() 是钝角三角形
是钝角三角形
【解析】试题分析: ![]() 设双曲线方程为
设双曲线方程为![]() ,由已知得
,由已知得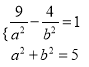 ,由此能求出双曲线的标准方程;
,由此能求出双曲线的标准方程;
![]() 不妨设点
不妨设点![]() 在双曲线的右支上,则
在双曲线的右支上,则![]() ,利用
,利用![]() ,求出
,求出![]() ,
, ![]() 的值,再由余弦定理可得
的值,再由余弦定理可得![]() ,即可得出结论。
,即可得出结论。
解析:(1)椭圆方程可化为![]() ,焦点在
,焦点在![]() 轴上,且
轴上,且![]()
故可设双曲线方程为![]() ,
,
则有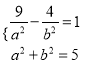
解得 ![]() ,
,
故双曲线的标准方程为![]() .
.
(2)不妨设![]() 在双曲线的右支上,
在双曲线的右支上,
则有|MF1|-|MF2|=![]() 又|MF1|+|MF2|=
又|MF1|+|MF2|=![]() ,
,
解得![]()
因此在![]() 中,
中, ![]() 边最长,
边最长,
由余弦定理可得
![]() .
.
所以![]() 为钝角,故
为钝角,故![]() 是钝角三角形.
是钝角三角形.
-
科目: 来源: 题型:
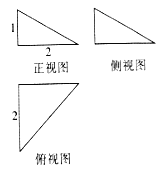
查看答案和解析>>【题目】如图是某几何体的三视图.
(1)求该几何体外接球的体积;
(2)求该几何体内切球的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设p:实数x满足
 ,其中a≠0,q:实数x满足
,其中a≠0,q:实数x满足 .
. (I)若a=1,且p∧q为真,求实数x的取值范围.
(II)若p是q的必要不充分条件,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四棱锥
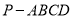 中,底面
中,底面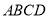 为矩形,
为矩形, 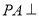 平面
平面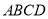 ,
, 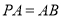 ,点
,点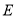 为
为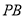 的中点.
的中点.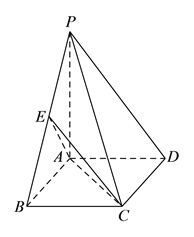
(
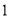 )求证:
)求证: 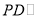 平面
平面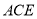 .
.(
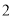 )求证:平面
)求证:平面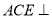 平面
平面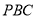 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
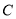 :
: 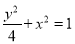 ,过点
,过点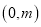 作圆
作圆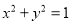 的切线交椭圆
的切线交椭圆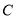 于
于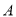 、
、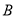 两点.
两点.(Ⅰ)求椭圆
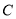 的焦点坐标和离心率;
的焦点坐标和离心率;(Ⅱ)将
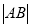 表示成
表示成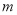 的函数,并求
的函数,并求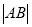 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
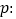 方程
方程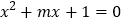 有两个不等的负根,
有两个不等的负根,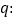 方程
方程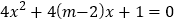 无实根,若“
无实根,若“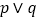 ”为真,“
”为真,“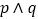 ”为假,求实数
”为假,求实数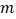 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】【河南省新乡市2017届高三上学期第一次调研】设
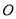 为坐标原点,已知椭圆
为坐标原点,已知椭圆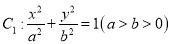 的离心率为
的离心率为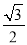 ,抛物线
,抛物线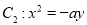 的准线方程为
的准线方程为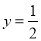 .
.(1)求椭圆
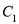 和抛物线
和抛物线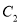 的方程;
的方程;(2)设过定点
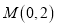 的直线
的直线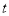 与椭圆
与椭圆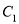 交于不同的两点
交于不同的两点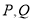 ,若
,若 在以
在以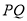 为直径的圆的外部,求直
为直径的圆的外部,求直线
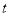 的斜率
的斜率 的取值范围.
的取值范围.
相关试题

