【题目】已知函数![]() (
(![]() ).
).
(1)若![]() 在
在![]() 处取到极值,求
处取到极值,求![]() 的值;
的值;
(2)若![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(3)求证:当![]() 时,
时, ![]() .
.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)根据极值的概念得到![]() ,可得到参数值;(2)转化为函数最值问题,研究函数的单调性,分
,可得到参数值;(2)转化为函数最值问题,研究函数的单调性,分![]() 时,
时,![]() 时,
时,![]() ,三种情况讨论单调性,使得最小值大于等于0即可;(3)由(1)知令
,三种情况讨论单调性,使得最小值大于等于0即可;(3)由(1)知令![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,给x赋值:2,3,4,5等,最终证得结果.
,给x赋值:2,3,4,5等,最终证得结果.
试题解析:(1)![]() ,
,
∵![]() 在
在![]() 处取到极值,
处取到极值,
∴![]() ,即
,即![]() ,∴
,∴![]() ,
,
经检验,![]() 时,
时,![]() 在
在![]() 处取到极小值.
处取到极小值.
(2)![]() ,令
,令![]() (
(![]() ),
),
1°当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,
,
∴![]() 时,
时,![]() ,不满足
,不满足![]() 在
在![]() 上恒成立.
上恒成立.
2°当![]() 时,二次函数
时,二次函数![]() 开口向上,对称轴为
开口向上,对称轴为![]() ,过
,过![]() .
.
①当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上恒成立,∴
上恒成立,∴![]() ,从而
,从而![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,∴
,∴![]() 时,
时,![]() 成立,满足
成立,满足![]() 在
在![]() 上恒成立;
上恒成立;
②当![]() ,即
,即![]() 时,存在
时,存在![]() ,使
,使![]() 时,
时, ![]() ,
,![]() 单调递减,
单调递减,![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
∴![]() ,又
,又![]() ,∴
,∴![]() ,故不满足题意.
,故不满足题意.
3°当![]() 时,二次函数
时,二次函数![]() 开口向下,对称轴为
开口向下,对称轴为![]() ,
, ![]() 在
在![]() 单调递减,
单调递减, ![]() ,
,
∴![]() ,
,![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,∴
,∴![]() 时,
时,![]() ,故不满足题意;综上所述,
,故不满足题意;综上所述, ![]() .
.
(3)证明:由(1)知令![]() ,当
,当![]() 时,
时, ![]() (当且仅当
(当且仅当![]() 时取“
时取“![]() ”),
”),
∴当![]() 时
时![]() .即当
.即当![]() 2,3,4,
2,3,4,![]() ,
,![]() ,有
,有
![]()
![]()
![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学在研究函数

 时,给出下面几个结论中正确的有( )
时,给出下面几个结论中正确的有( )A.
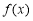 的图象关于点
的图象关于点 对称B.若
对称B.若 ,则
,则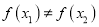
C.
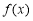 的值域为
的值域为 D.函数
D.函数 有三个零点
有三个零点 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分14分)如图,已知椭圆
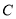 :
: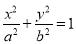 ,其左右焦点为
,其左右焦点为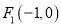 及
及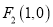 ,过点
,过点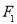 的直线交椭圆
的直线交椭圆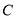 于
于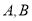 两点,线段
两点,线段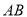 的中点为
的中点为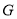 ,
,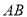 的中垂线与
的中垂线与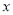 轴和
轴和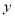 轴分别交于
轴分别交于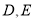 两点,且
两点,且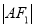 、
、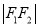 、
、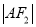 构成等差数列.
构成等差数列.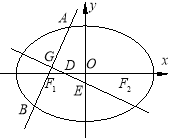
(1)求椭圆
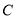 的方程;
的方程;(2)记△
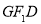 的面积为
的面积为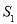 ,△
,△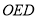 (
(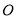 为原点)的面积为
为原点)的面积为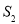 .试问:是否存在直线
.试问:是否存在直线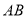 ,使得
,使得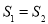 ?说明理由.
?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】2018年10月24日,世界上最长的跨海大桥一港珠澳大桥正式通车
 在一般情况下,大桥上的车流速度
在一般情况下,大桥上的车流速度 单位:千米
单位:千米 时
时 是车流密度
是车流密度 单位:辆
单位:辆 千米
千米 的函数
的函数 当桥上的车流密度达到220辆
当桥上的车流密度达到220辆 千米时,将造成堵塞,此时车流速度为0;当车流密度不超过20辆
千米时,将造成堵塞,此时车流速度为0;当车流密度不超过20辆 千米时,车流速度为100千米
千米时,车流速度为100千米 时,研究表明:当
时,研究表明:当 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数. Ⅰ
Ⅰ 当
当 时,求函数
时,求函数 的表达式;
的表达式; Ⅱ
Ⅱ 当车流密度x为多大时,车流量
当车流密度x为多大时,车流量 单位时间内通过桥上某观测点的车辆数,单位:辆
单位时间内通过桥上某观测点的车辆数,单位:辆 时
时 可以达到最大?并求出最大值.
可以达到最大?并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x(lnx-ax)有两个极值点,则实数a的取值范围是( )
A. (-∞,0) B.
 C. (0,1) D. (0,+∞)
C. (0,1) D. (0,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数
 ,定义域为
,定义域为 的函数
的函数 是偶函数,其中
是偶函数,其中 为自然对数的底数.
为自然对数的底数.(Ⅰ)求实数
 值;
值;(Ⅱ)判断该函数
 在
在 上的单调性并用定义证明;
上的单调性并用定义证明;(Ⅲ)是否存在实数
 ,使得对任意的
,使得对任意的 ,不等式
,不等式 恒成立.若存在,求出实数
恒成立.若存在,求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
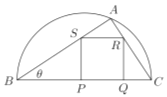
查看答案和解析>>【题目】校园准备绿化一块直径为
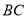 的半圆形空地,点
的半圆形空地,点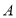 在半圆圆弧上,△
在半圆圆弧上,△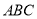 外的地方种草,△
外的地方种草,△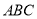 的内接正方形
的内接正方形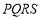 为一水池(
为一水池(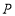 ,
,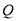 在
在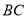 边上),其余地方种花,若
边上),其余地方种花,若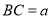 ,
, 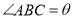 ,设△
,设△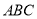 的面积为
的面积为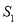 ,正方形面积为
,正方形面积为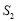 ;
;
(1)用
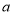 和
和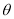 表示
表示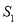 和
和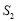 ;
;(2)当
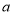 固定,
固定,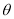 变化时,求
变化时,求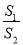 最小值及此时的角
最小值及此时的角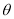 ;
;
相关试题

