搜索
【题目】已知函数f（x）=sinx﹣x，若f（cos2θ+2msinθ）+f（﹣2﹣2m）＞0对任意的θ∈（0， 
）恒成立，则实数m的取值范围为 ．
参考答案：
【答案】[﹣ 
，+∞）
【解析】解：由f（x）=sinx﹣x可知，f（x）定义域为R，且为奇函数；
∵f'（x）=cosx﹣1≤0，则f（x）在R上单调递减；
f（cos2θ+2msinθ）+f（﹣2﹣2m）＞0 即：f（cos2θ+2msinθ）＞f（2m+2）；
根据函数单调性有：cos2θ+2msinθ＜2m+2 ①；
sinθ=t∈（0，1），1﹣t＞0，①式则：1﹣t2+2mt＜2m+2；
﹣1﹣t2＜2m（1﹣t）；
m＞ 
=﹣ [（1﹣t）+ 
﹣2]
∵u=（1﹣t）+ ﹣2 在（0，1）上单调递减，u（0）=1
∴m 
﹣
所以答案是：[﹣ ，+∞）
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点，需要掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知a，b为正实数，函数f（x）=ax3+bx+2x在[0，1]上的最大值为4，则f（x）在[﹣1，0]上的最小值为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂有25周岁以上（含25周岁）工人300名，25周岁以下工人200名．为了研究工人的日平均生产量是否与年龄有关，现采用分层抽样的方法，从中抽取了100名工人，先统计了他们某月的日平均生产件数，然后按工人年龄在“25周岁以上（含25周岁）”和“25周岁以下”分为两组，再将两组工人的日平均生产件数分成5组：
，
，
，
，
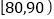，分别加以统计，得到如图所示的频率分布直方图．
（1）根据“25周岁以上组”的频率分布直方图，求25周岁以上组工人日平均生产件数的中位数的估计值（四舍五入保留整数）；
（2）从样本中日平均生产件数不足60件的工人中随机抽取2人，求至多抽到一名“25周岁以下组”工人的概率。
-
科目： 来源： 题型：
查看答案和解析>>【题目】我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准
（吨），一位居民的月用水量不超过的部分按平价收费，超出的部分按议价收费。为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照
，
…，
分成9组，制成了如图所示的频率分布直方图。
（1）求直方图中
的值；（2）设该市有60万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；
（3）若该市政府希望使82%的居民每月的用水量不超过标准
（吨），估计的值，并说明理由。 -
科目： 来源： 题型：
查看答案和解析>>【题目】设集合A={x|﹣1≤x≤2}，B={x|x2﹣x+（m﹣m2）＜0}．
（1）当m＜
时，化简集合B；
（2）p：x∈A，命题q：x∈B，且命题p是命题q的必要不充分条件，求实数m的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】某大学在开学季准备销售一种盒饭进行试创业，在一个开学季内，每售出1盒该盒饭获利润10元，未售出的产品，每盒亏损5元．根据历史资料，得到开学季市场需求量的频率分布直方图，如图所示．该同学为这个开学季购进了150盒该产品，以x（单位：盒，
）表示这个开学季内的市场需求量，y（单位：元）表示这个开学季内经销该产品的利润．
（1）根据直方图估计这个开学季内市场需求量x的平均数和众数；
（2）将y表示为x的函数；
（3）根据频率分布直方图估计利润y不少于1050元的概率.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=sin2ωx+2
sinωxcosωx﹣cos2ωx（ω＞0），f（x）的图象相邻两条对称轴的距离为 
．
（1）求f（ ）的值；
（2）将f（x）的图象上所有点向左平移m（m＞0）个长度单位，得到y=g（x）的图象，若y=g（x）图象的一个对称中心为（
，0），当m取得最小值时，求g（x）的单调递增区间．
相关试题
