【题目】已知函数![]() (
(![]() 是自然对数的底数)与
是自然对数的底数)与![]() 的图象上存在关于
的图象上存在关于![]() 轴对称的点,则实数
轴对称的点,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】根据题意,若函数f(x)=﹣x3+1+a(![]() ≤x≤e,e是自然对数的底)与g(x)=3lnx的图象上存在关于x轴对称的点,
≤x≤e,e是自然对数的底)与g(x)=3lnx的图象上存在关于x轴对称的点,
则方程﹣x3+1+a=﹣3lnx在区间[![]() ,e]上有解,
,e]上有解,
﹣x3+1+a=﹣3lnxa+1=x3﹣31nx,即方程a+1=x3﹣31nx在区间[![]() ,e]上有解,
,e]上有解,
设函数g(x)=x3﹣31nx,其导数g′(x)=3x2﹣![]() =
=![]() ,
,
又由x∈[![]() ,e],g′(x)=0在x=1有唯一的极值点,
,e],g′(x)=0在x=1有唯一的极值点,
分析可得:当![]() ≤x≤1时,g′(x)<0,g(x)为减函数,
≤x≤1时,g′(x)<0,g(x)为减函数,
当1≤x≤e时,g′(x)>0,g(x)为增函数,
故函数g(x)=x3﹣31nx有最小值g(1)=1,
又由g(![]() )=
)=![]() +3,g(e)=e3﹣3;比较可得:g(
+3,g(e)=e3﹣3;比较可得:g(![]() )<g(e),
)<g(e),
故函数g(x)=x3﹣31nx有最大值g(e)=e3﹣3,
故函数g(x)=x3﹣31nx在区间[![]() ,e]上的值域为[1,e3﹣3];
,e]上的值域为[1,e3﹣3];
若方程a+1=x3﹣31nx在区间[![]() ,e]上有解,
,e]上有解,
必有1≤a+1≤e3﹣3,则有0≤a≤e3﹣4,
即a的取值范围是[0,e3﹣4];
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下判断正确的个数是( )
①相关系数
 值越小,变量之间的相关性越强.
值越小,变量之间的相关性越强.②命题“存在
 ”的否定是“不存在
”的否定是“不存在 ”.
”.③“
 ”为真是“
”为真是“ ”为假的必要不充分条件.
”为假的必要不充分条件.④若回归直线的斜率估计值是1.23,样本点的中心为(4,5),则回归直线方程是
 .
.A. 4 B. 2 C. 3 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=a(
 )x+bx2+cx(α∈R,b≠0,c∈R),若{x|f(x)=0}={x|f(f(x))=0}≠,则实数c的取值范围为( )
)x+bx2+cx(α∈R,b≠0,c∈R),若{x|f(x)=0}={x|f(f(x))=0}≠,则实数c的取值范围为( )
A.(0,4)
B.[0,4]
C.(0,4]
D.[0,4) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知θ∈(
 ,
,  ),若存在实数x,y同时满足
),若存在实数x,y同时满足  =
=  ,
,  +
+ 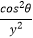 =
=  ,则tanθ的值为 .
,则tanθ的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 为偶函数,当
为偶函数,当 时,
时, ,若函数
,若函数 恰有一个零点,则实数
恰有一个零点,则实数 的取值集合是( )
的取值集合是( )A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sin
 +e﹣|x﹣1| , 有下列四个结论:
+e﹣|x﹣1| , 有下列四个结论:
①图象关于直线x=1对称;
②f(x)的最大值是2;
③f(x)的最大值是﹣1,;
④f(x)在区间[﹣2015,2015]上有2015个零点.
其中正确的结论是(写出所有正确的结论序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=﹣x2+ax+1﹣lnx.
(1)当a=3时,求函数f(x)的单调递增区间;
(2)若f(x)在区间(0, )上是减函数,求实数a的取值范围.
)上是减函数,求实数a的取值范围.
相关试题

