【题目】在如图所示的空间几何体中,平面![]() 平面
平面![]() ,
,![]() 与
与![]() 都是边长为2的等边三角形,
都是边长为2的等边三角形,![]() ,
,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,且点E在平面
,且点E在平面![]() 上的射影落在
上的射影落在![]() 的平分线上.
的平分线上.
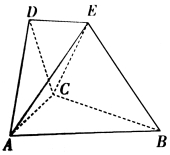
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,可证得
,可证得![]() 平面
平面![]() ,作
,作![]() 平面
平面![]() ,那么
,那么![]() ,通过证明四边形
,通过证明四边形![]() 是平行四边形,证得
是平行四边形,证得![]() ,由线面平行的判定定理证明;(2)以
,由线面平行的判定定理证明;(2)以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴的正方向建立空间直角坐标系,求出平面
轴的正方向建立空间直角坐标系,求出平面![]() 的一个法向量和平面
的一个法向量和平面![]() 的法向量的夹角,即得二面角
的法向量的夹角,即得二面角![]() 的余弦值.
的余弦值.
试题解析:(1)由题意知![]() 、
、![]() 为边长2的等边
为边长2的等边![]() 取
取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
则![]() ,
,![]() .又平面
.又平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,作
,作![]() 平面
平面![]() ,
,
那么![]() ,根据题意,点
,根据题意,点![]() 落在
落在![]() 上,
上,![]() 和平面
和平面![]() 所成的角为
所成的角为![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() .
.
![]() 平面ABC,
平面ABC,![]() 平面
平面![]() ,
, ![]() 平面
平面![]() .
.
(2)建立空间直角坐标系![]() ,则
,则![]() ,
,![]() ,
,![]() ,
, ![]()
![]()
平面![]() 的一个法向量为
的一个法向量为![]()
设平面![]() 的法向量
的法向量![]() 则
则

取![]() ,
,![]()
![]() ,又由图知,所求二面角的平面角是锐角,二面角
,又由图知,所求二面角的平面角是锐角,二面角![]() 的余弦值为
的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的中心在坐标原点,左、右焦点
的中心在坐标原点,左、右焦点 分别在
分别在 轴上,离心率为
轴上,离心率为 ,在其上有一动点
,在其上有一动点 ,
, 到点
到点 距离的最小值是1.过
距离的最小值是1.过 作一个平行四边形,顶点
作一个平行四边形,顶点 都在椭圆
都在椭圆 上,如图所示.
上,如图所示.
(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)判断
 能否为菱形,并说明理由.
能否为菱形,并说明理由.(Ⅲ)当
 的面积取到最大值时,判断
的面积取到最大值时,判断 的形状,并求出其最大值.
的形状,并求出其最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
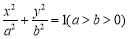 的离心率为
的离心率为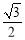 ,以椭圆的一个短轴端点及两个焦点构成的三角形的面积为
,以椭圆的一个短轴端点及两个焦点构成的三角形的面积为 ,圆C方程为
,圆C方程为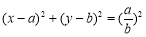 .
.(1)求椭圆及圆C的方程;
(2)过原点O作直线l与圆C交于A,B两点,若
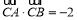 ,求直线l的方程.
,求直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,已知F1、F2分别是椭圆C:
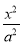 +
+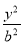 =1(a>b>0)的左、右焦点,且右焦点F2的坐标为(
=1(a>b>0)的左、右焦点,且右焦点F2的坐标为(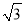 ,0),点(
,0),点(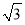 ,
,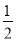 )在椭圆C上.
)在椭圆C上.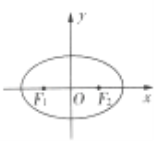
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)在椭圆C上任取一点P,点Q在PO的延长线上,且
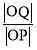 =2.
=2.(1)当点P在椭圆C上运动时,求点Q形成的轨迹E的方程;
(2)若过点P的直线l:y=x+m交(1)中的曲线E于A,B两点,求△ABQ面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三共有2000名学生参加广安市联考,现随机抽取100名学生的成绩(单位:分),并列成如下表所示的频数分布表:
组别
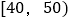
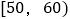
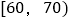
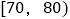
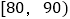
频数
6
18
28
26
17
5
(1)试估计该年级成绩
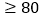 分的学生人数;
分的学生人数;(2)已知样本中成绩在
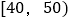 中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.
中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】设p:实数x满足
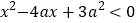 ,其中
,其中 ,命题
,命题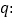 实数
实数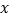 满足
满足|x-3|≤1 .
(1)若
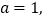 且
且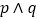 为真,求实数
为真,求实数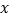 的取值范围;
的取值范围;(2)若
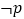 是
是
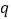 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
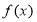 满足:对任意
满足:对任意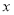 ,
,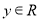 ,都有
,都有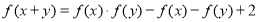 成立,且
成立,且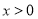 时,
时,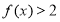 .
.(1)求
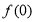 的值,并证明:当
的值,并证明:当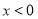 时,
时,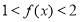 ;
;(2)判断
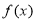 的单调性并加以证明;
的单调性并加以证明;(3)若函数
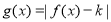 在
在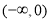 上递减,求实数
上递减,求实数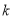 的取值范围.
的取值范围.
相关试题

