【题目】若<<0,则下列不等式:①<;②|a|+b>0;③a->b-;④lna2>lnb2中,正确的是( )
(A)①④ (B)②③ (C)①③ (D)②④
参考答案:
【答案】D
【解析】先由![]() <
<![]() <0得到a与b的大小关系,再根据不等式的性质,对各个不等式进行逐一判断.
<0得到a与b的大小关系,再根据不等式的性质,对各个不等式进行逐一判断.
由![]() <
<![]() <0,可知b<a<0.
<0,可知b<a<0.
①中,a+b<0,ab>0,所以![]() <0,
<0,![]() >0.
>0.
故有![]() <
<![]() ,即①正确.
,即①正确.
②中,∵b<a<0,∴-b>-a>0,故-b>|a|,即|a|+b<0,故②错误.
③中,∵b<a<0,即0>a>b,
又∵![]() <
<![]() <0,∴-
<0,∴-![]() >-
>-![]() >0,
>0,
∴a-![]() >b-
>b-![]() ,故③正确.
,故③正确.
④中,∵b<a<0,根据y=x2在(-∞,0)上为单调递减函数,可得b2>a2>0,而y=lnx在定义域上为增函数.∴lnb2>lna2,故④错,综上分析,②④错误,①③正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 为奇函数,
为奇函数,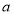 为常数.
为常数.(Ⅰ)求实数
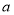 的值;
的值;(Ⅱ)求函数
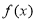 的单调区间;
的单调区间;(Ⅲ)若对于区间
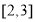 上的每一个
上的每一个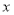 值,不等式
值,不等式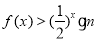 恒成立,求实数
恒成立,求实数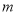 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
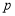 :实数
:实数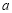 满足不等式
满足不等式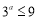 ,
,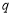 :函数
:函数 无极值点.
无极值点.(1)若“
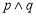 ”为假命题,“
”为假命题,“ ”为真命题,求实数
”为真命题,求实数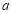 的取值范围;
的取值范围;(2)已知. “
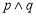 ”为真命题,并记为
”为真命题,并记为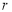 ,且
,且 :
: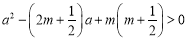 ,若
,若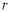 是
是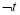 的必要不充分条件,求实数
的必要不充分条件,求实数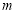 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
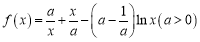 .
.(1)求函数
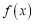 的单调区间和极值;
的单调区间和极值;(2)证明:当
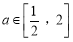 时,函数
时,函数 没有零点(提示:
没有零点(提示: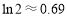 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲、乙两煤矿每年的产量分别为200万吨和300万吨,需经过东车站和西车站两个车站运往外地,东车站每年最多能运280万吨煤,西车站每年最多能运360万吨煤,甲煤矿运往东车站和西车站的运费价格分别为1元/吨和1.5元/吨,乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨.要使总运费最少,煤矿应怎样编制调运方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
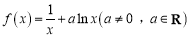 .
.(1)若
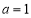 ,求函数
,求函数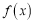 的极值和单调区间;
的极值和单调区间;(2)若在区间
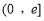 上至少存在一点
上至少存在一点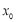 ,使得
,使得 成立,求实数
成立,求实数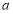 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
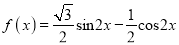 ,
, 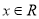 .
.(1)若对任意
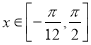 ,都有
,都有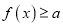 成立,求
成立,求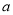 的值值范围;
的值值范围;(2)若先将
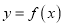 的图象上每个点纵坐标不变,横坐标变为原来的2倍,然后再向左平移
的图象上每个点纵坐标不变,横坐标变为原来的2倍,然后再向左平移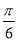 个单位得到函数
个单位得到函数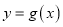 的图象,求函数
的图象,求函数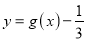 在区间
在区间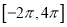 内的所有零点之和.
内的所有零点之和.
相关试题

