【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间和极值;
的单调区间和极值;
(2)证明:当![]() 时,函数
时,函数![]() 没有零点(提示:
没有零点(提示:![]() ).
).
参考答案:
【答案】(1)单调增区间为![]() ,单调减区间为
,单调减区间为![]() ,极小值为
,极小值为![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)对函数![]() 进行化简求导得
进行化简求导得![]() .利用导数工具可得:当
.利用导数工具可得:当![]() 时,
时,![]() 取得极小值
取得极小值![]() ;(2)由(1)可知
;(2)由(1)可知![]() 取得极小值,亦即最小值为:
取得极小值,亦即最小值为:
![]() ,又
,又![]()
![]()
![]() ,设
,设![]()
![]() ,利用导数工具得
,利用导数工具得![]() 有唯一的零点
有唯一的零点![]() ,使得
,使得![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.又由于
上单调递减.又由于![]()
![]()
![]() 恒成立
恒成立![]()
![]() 恒成立
恒成立![]()
![]() 恒成立
恒成立![]() 当
当![]() 时,函数
时,函数![]() 没有零点.
没有零点.
试题解析:(1)因为![]() ,
,
所以![]() .
.
因为![]() ,所以当
,所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
所以函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
当![]() 时,
时,![]() 取得极小值
取得极小值![]() .
.
(2)由(1)可知:当![]() 时,
时,![]() 取得极小值,亦即最小值.
取得极小值,亦即最小值.
![]() ,又因为
,又因为![]() ,所以
,所以![]() ,
,
设![]()
![]() ,则
,则![]() .
.
因为![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,
,
所以![]() 有唯一的零点
有唯一的零点![]() ,使得
,使得![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
又由于![]() .
.
所以![]() 恒成立,从而
恒成立,从而![]() 恒成立,则
恒成立,则![]() 恒成立.
恒成立.
所以当![]() 时,函数
时,函数![]() 没有零点.
没有零点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设复数z=2m+(4-m2)i,当实数m取何值时,复数z对应的点:
(1)位于虚轴上?
(2)位于一、三象限?
(3)位于以原点为圆心,以4为半径的圆上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 为奇函数,
为奇函数,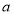 为常数.
为常数.(Ⅰ)求实数
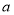 的值;
的值;(Ⅱ)求函数
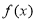 的单调区间;
的单调区间;(Ⅲ)若对于区间
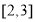 上的每一个
上的每一个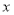 值,不等式
值,不等式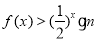 恒成立,求实数
恒成立,求实数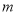 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
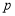 :实数
:实数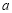 满足不等式
满足不等式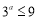 ,
,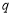 :函数
:函数 无极值点.
无极值点.(1)若“
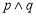 ”为假命题,“
”为假命题,“ ”为真命题,求实数
”为真命题,求实数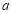 的取值范围;
的取值范围;(2)已知. “
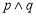 ”为真命题,并记为
”为真命题,并记为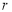 ,且
,且 :
: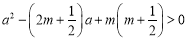 ,若
,若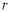 是
是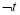 的必要不充分条件,求实数
的必要不充分条件,求实数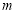 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】若<<0,则下列不等式:①<;②|a|+b>0;③a->b-;④lna2>lnb2中,正确的是( )
(A)①④ (B)②③ (C)①③ (D)②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲、乙两煤矿每年的产量分别为200万吨和300万吨,需经过东车站和西车站两个车站运往外地,东车站每年最多能运280万吨煤,西车站每年最多能运360万吨煤,甲煤矿运往东车站和西车站的运费价格分别为1元/吨和1.5元/吨,乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨.要使总运费最少,煤矿应怎样编制调运方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
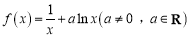 .
.(1)若
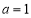 ,求函数
,求函数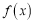 的极值和单调区间;
的极值和单调区间;(2)若在区间
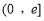 上至少存在一点
上至少存在一点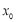 ,使得
,使得 成立,求实数
成立,求实数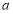 的取值范围.
的取值范围.
相关试题

