【题目】如图,在棱长为![]() 的正方体
的正方体![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.

(![]() )求异面直线
)求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
(![]() )在棱
)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
参考答案:
【答案】(![]() )
)![]() .(
.(![]() )存在,
)存在,![]() .
.
【解析】试题分析:(1)取![]() 中点
中点![]() ,根据平行公理得
,根据平行公理得![]() 即为异面直线
即为异面直线![]() 与
与![]() 所成角,再根据直角三角形解角,(2)连结
所成角,再根据直角三角形解角,(2)连结![]() ,
,![]() 交于点
交于点![]() ,则根据三垂线定理得
,则根据三垂线定理得![]() 为二面角
为二面角![]() 的平面角,再根据直角三角形解得
的平面角,再根据直角三角形解得![]() .
.
试题解析:(![]() )取
)取![]() 中点
中点![]() ,连结
,连结![]() ,
,
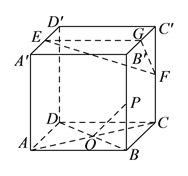
又∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
连结![]() ,则
,则![]() 即为异面直线
即为异面直线![]() 与
与![]() 所成角,
所成角,
∵![]() 为
为![]() 中点,正方体边长为
中点,正方体边长为![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
故异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
(![]() )存在,在棱
)存在,在棱![]() 上取一点
上取一点![]() ,
,
由题意可知,![]() 面
面![]() ,
,
连结![]() ,
,![]() 交于点
交于点![]() ,易知
,易知![]() ,
,![]() ,
,
连结![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角,
的平面角,
当![]() 时,即
时,即![]() ,
,
解得![]() ,
,
∴当![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①第二象限角比第一象限角大;②设
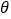 是第二象限角,则
是第二象限角,则 ;③三角形的内角是第一象限角或第二象限角;④函数
;③三角形的内角是第一象限角或第二象限角;④函数 是最小正周期为
是最小正周期为 的周期函数;⑤在△ABC中,若
的周期函数;⑤在△ABC中,若 ,则A>B.其中正确的是___________ (写出所有正确说法的序号)
,则A>B.其中正确的是___________ (写出所有正确说法的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=(5
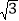 cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+
cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+ .
.(1) 求函数f (x)的最小正周期和对称中心;
(2) 当
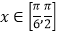 时,求函数f(x)的值域;
时,求函数f(x)的值域;(3) 该函数y=f (x)的图象可由
 的图象经过怎样的变换得到?
的图象经过怎样的变换得到? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的焦点到准线的距离为
的焦点到准线的距离为 ,直线
,直线 与抛物线
与抛物线 交于
交于 两点,过这两点分别作抛物线
两点,过这两点分别作抛物线 的切线,且这两条切线相交于点
的切线,且这两条切线相交于点 .
.(1)若
 的坐标为
的坐标为 ,求
,求 的值;
的值;(2)设线段
 的中点为
的中点为 ,点
,点 的坐标为
的坐标为 ,过
,过 的直线
的直线 与线段
与线段 为直径的圆相切,切点为
为直径的圆相切,切点为 ,且直线
,且直线 与抛物线
与抛物线 交于
交于 两点,求
两点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 ,
,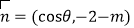 ,函数
,函数 的最小值为
的最小值为
(1)当
 时,求
时,求 的值;
的值; (2)求
 ;
;(3)已知函数
 为定义在R上的增函数,且对任意的
为定义在R上的增函数,且对任意的 都满足
都满足
问:是否存在这样的实数m,使不等式

 +
+ 对所有
对所有
恒成立,若存在,求出m的取值范围;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解甲、乙两校高三年级学生某次期末联考地理成绩情况,从这两学校中分别随机抽取30名高三年级的地理成绩(百分制)作为样本,样本数据的茎叶图如图所示:

(Ⅰ)若乙校高三年级每位学生被抽取的概率为0.15,求乙校高三年级学生总人数;
(Ⅱ)根据茎叶图,分析甲、乙两校高三年级学生在这次联考中地理成绩;
(Ⅲ)从样本中甲、乙两校高三年级学生地理成绩不及格(低于60分为不及格)的学生中随机抽取2人,求至少抽到一名乙校学生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C:y2=4x,焦点为F,过点P(﹣1,0)作斜率为k(k>0)的直线l与抛物线C交于A,B两点,直线AF,BF分别交抛物线C于M,N两点,若
 +
+ 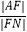 =18,则k= .
=18,则k= .
相关试题

