【题目】某班主任对全班50名学生作了一次调查,所得数据如表:
认为作业多 | 认为作业不多 | 总计 | |
喜欢玩电脑游戏 | 18 | 9 | 27 |
不喜欢玩电脑游戏 | 8 | 15 | 23 |
总计 | 26 | 24 | 50 |
由表中数据计算得到K2的观测值k≈5.059,于是________(填“能”或“不能”)在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关.
参考答案:
【答案】不能
【解析】查表知若要在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关,则临界值k0=6.635.本题中,k≈5.059<6.635,所以不能在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于数25,规定第1次操作为23+53=133,第2次操作为13+33+33=55,如此反复操作,则第2 017次操作后得到的数是( )
A. 25 B. 250
C. 55 D. 133
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用独立性检验来考虑两个分类变量X和Y是否有关系时,通过查阅临界值表来确定推断“X与Y有关系”的可信度,如果k>5.024,那么就推断“X和Y有关系”,这种推断犯错误的概率不超过( )
A. 0.25 B. 0.75
C. 0.025 D. 0.975
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了普及环保知识增强环保意识,某校从理工类专业甲班抽取60人,从文史类乙班抽取50人参加环保知识测试.
(1)根据题目条件完成下面2×2列联表,并据此判断你是否有99%的把握认为环保知识与专业有关?
优秀
非优秀
总计
甲班
乙班
30
总计
60
(2)为参加上级举办的环保知识竞赛,学校举办预选赛,预选赛答卷满分100分,优秀的同学得60分以上通过预选,非优秀的同学得80分以上通过预选,若每位同学得60分以上的概率为

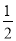 ,得80分以上的概率为
,得80分以上的概率为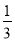 ,现已知甲班有3人参加预选赛,其中1人为优秀学生,若随机变量X表示甲班通过预选的人数,
,现已知甲班有3人参加预选赛,其中1人为优秀学生,若随机变量X表示甲班通过预选的人数,求X的分布列及期望E(X).
附:
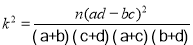 , n=a+b+c+d
, n=a+b+c+dP(K2>k0)
0.100
0.050
0.025
0.010[
0.005
k0
2.706
3.84
5.02
6.635
7.879
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a=log0.50.2,b=log20.2,c=20.2,则a,b,c的大小关系是( )
A. a<b<c B. b<c<a C. b<a<c D. c<b<a
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程
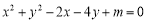 .
.(1)若此方程表示圆,求
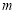 的取值范围;
的取值范围;(2)若(1)中的圆与直线
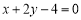 相交于
相交于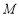 ,
,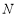 两点,且
两点,且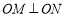 (
(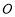 为坐标原点),求
为坐标原点),求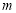 ;
;(3)在(2)的条件下,求以
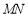 为直径的圆的方程.
为直径的圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】
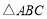 中,
中,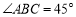 ,
,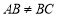 ,
,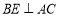 于点
于点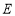 ,
,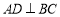 于点
于点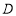 .
.(1)如图1,作
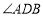 的角平分线
的角平分线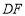 交
交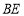 于点
于点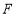 ,连接
,连接 .求证:
.求证: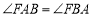 ;
;(2)如图2,连接
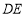 ,点
,点 与点
与点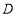 关于直线
关于直线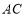 对称,连接
对称,连接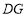 、
、 .
.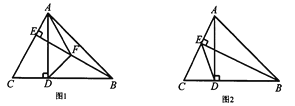
①依据题意补全图形;
②用等式表示线段
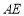 、
、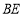 、
、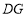 之间的数量关系,并加以证明.
之间的数量关系,并加以证明.
相关试题

