【题目】已知椭圆![]() 的方程为
的方程为![]() (
(![]() )的离心率为
)的离心率为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,若椭圆
,若椭圆![]() 与圆
与圆![]() 相交于
相交于![]() ,
, ![]() 两点,且线段
两点,且线段![]() 恰好为圆
恰好为圆![]() 的直径.
的直径.
(1)求直线![]() 的方程;
的方程;
(2)求椭圆![]() 的标准方程.
的标准方程.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1) 由椭圆![]() 的离心率为
的离心率为![]() ,可设椭圆
,可设椭圆![]() 的方程为
的方程为![]() ,设
,设![]() ,
, ![]() ,由线段
,由线段![]() 恰好为圆
恰好为圆![]() 的直径可得
的直径可得![]() ,
, ![]() ,由于
,由于![]() ,
, ![]() ,两式相减,并整理得
,两式相减,并整理得![]() ,∴
,∴![]() ,根据点斜式可求得直线
,根据点斜式可求得直线![]() 的方程;(2)由(1)知
的方程;(2)由(1)知![]() ,代入
,代入![]() 并整理得,
并整理得, ![]() ,根据弦长公式列方程可得
,根据弦长公式列方程可得![]() ,从而得
,从而得![]() ,进而可得椭圆
,进而可得椭圆![]() 的标准方程.
的标准方程.
试题解析:(1)由![]() 得,
得, ![]()
∴![]() ,即
,即![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() ,
,
设![]() ,
, ![]() ,∵线段
,∵线段![]() 恰好为圆
恰好为圆![]() 的直径,
的直径,
∴线段![]() 的中点恰好为圆心
的中点恰好为圆心![]() ,于是有
,于是有![]() ,
, ![]() ,
,
由于![]() ,
, ![]() ,两式相减,并整理得,
,两式相减,并整理得,
![]()
有![]() ,∴
,∴![]()
∴直线![]() 的方程为
的方程为![]() ,即
,即![]() 。
。
(2)解:由(1)知![]() ,代入
,代入![]() 并整理得,
并整理得,
![]() ,
,
∵椭圆![]() 与圆
与圆![]() 相交于
相交于![]() ,
, ![]() 两点,
两点,
∴![]() ,解得
,解得![]() ,
,
于是![]() ,
, ![]()
依题意, ![]() ,
,
而![]()
![]()
∴![]()
解得![]() ,满足
,满足![]()
∴![]()
∴所求椭圆![]() 的标准方程
的标准方程![]() .
.
【方法点晴】本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系和“点差法”的应用,属于难题. 用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在![]() 轴上,还是在
轴上,还是在![]() 轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程
轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程![]() 或
或![]()
![]() ;③找关系:根据已知条件,建立关于
;③找关系:根据已知条件,建立关于![]() 、
、![]() 、
、![]() 的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题
 :
:  表示双曲线,命题
表示双曲线,命题 :
:  表示椭圆。
表示椭圆。(1)若命题
 与命题
与命题 都为真命题,则
都为真命题,则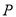 是
是 的什么条件?
的什么条件?(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和“既不充分也不必要条件”中的哪一个)
(2)若
 为假命题,且
为假命题,且 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面上的三点
 、
、 、
、 .
.(1)求以
 、
、 为焦点且过点
为焦点且过点 的椭圆的标准方程;
的椭圆的标准方程;(2)设点
 、
、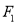 、
、 关于直线
关于直线 的对称点分别为
的对称点分别为 、
、 、
、 ,求以
,求以 、
、 为焦点且过点
为焦点且过点 的双曲线的标准方程.
的双曲线的标准方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 :
:  (
( )的焦点为
)的焦点为 ,点
,点 在抛物线
在抛物线 上,且
上,且 ,直线
,直线 与抛物线
与抛物线 交于
交于 ,
, 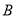 两点,
两点,  为坐标原点.
为坐标原点.(1)求抛物线
 的方程;
的方程;(2)求
 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的中心在原点,离心率为
的中心在原点,离心率为 ,右焦点到直线
,右焦点到直线 的距离为2.
的距离为2.(1)求椭圆
 的方程;
的方程;(2)椭圆下顶点为
 ,直线
,直线 (
( )与椭圆相交于不同的两点
)与椭圆相交于不同的两点 ,当
,当 时,求
时,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】随机掷两枚质地均匀的骰子,它们向上的点数之和不超过5的概率记为p1,点数之和大于5的概率记为p2,点数之和为偶数的概率记为p3,则( )
A. p1<p2<p3 B. p2<p1<p3
C. p1<p3<p2 D. p3<p1<p2
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数
 有以下说法:
有以下说法:①
 是
是 的极值点.
的极值点.②当
 时,
时,  在
在 上是减函数.
上是减函数. ③
 的图像与
的图像与 处的切线必相交于另一点.
处的切线必相交于另一点. ④当
 时,
时,  在
在 上是减函数.
上是减函数.其中说法正确的序号是_______________.
相关试题

