【题目】判断下列函数的奇偶性.
(1)f(x)=x2-|x|+1,x∈[-1,4]; (2)f(x)= ;
;
(3)f(x)=![]() ; (4)f(x)=
; (4)f(x)=
参考答案:
【答案】见解析
【解析】(1)虽然f(-x)=f(x),但定义域不关于原点对称,
故f(x)=x2-|x|+1,x∈[-1,4]是非奇非偶函数.
(2)由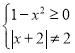 得-1≤x<0,或0<x≤1.
得-1≤x<0,或0<x≤1.
故函数f(x)的定义域为[-1,0)∪(0,1],关于原点对称,
且有x+2>0.从而有f(x)=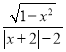 =
=![]() =
=![]() ,
,
于是f(-x)=-![]() =-f(x).故函数f(x)为奇函数.
=-f(x).故函数f(x)为奇函数.
(3)∵![]() ≥0,∴-1≤x<1.
≥0,∴-1≤x<1.
∴定义域不关于原点对称.∴f(x)为非奇非偶函数.
(4)当x>0时,x<0 ,f(-x)=(-x)2+(-x)=x2-x;
当x<0时,x>0,f(-x)=-(-x)2+(-x)=-x2-x.
∴f(-x)=-f(x),∴f(x)是奇函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂今年拟举行促销活动,经调查测算,该厂产品的年销售量(即该厂的年产量)x(万件)与年促销费m(万元)(m≥0)满足x=3-
 .已知今年生产的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
.已知今年生产的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).(1)将今年该产品的利润y(万元)表示为年促销费m(万元)的函数;
(2)求今年该产品利润的最大值,此时促销费为多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
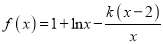 ,其中
,其中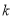 为常数.
为常数.(1)若
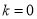 ,求曲线
,求曲线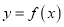 在点
在点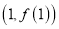 处的切线方程;
处的切线方程;(2)若
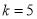 ,求
,求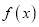 零点的个数;
零点的个数;(3)若
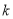 为整数,且当
为整数,且当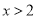 时,
时, 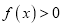 恒成立,求
恒成立,求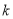 的最大值.
的最大值.(参考数据
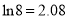 ,
, 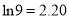 ,
, 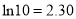 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】设A={x|x2+8x=0},B={x|x2+2(a+2)x+a2-4=0},其中a∈R.如果A∩B=B,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
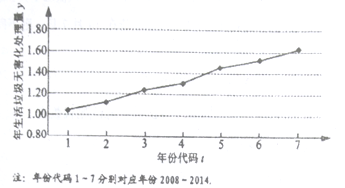
(1)由折线图看出,可用线性回归模型拟合
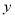 与
与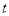 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;(2)建立
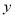 关于
关于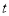 的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.参考数据:
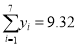 ,
, 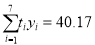 ,
, 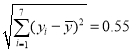 ,
, 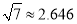 .
.参考公式:相关系数
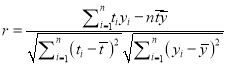
回归方程
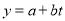 中,
中, 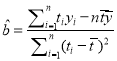 ,
, 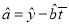 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业拟生产一种如图所示的圆柱形易拉罐(上下底面及侧面的厚度不计).易拉罐的体积为
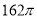
 ,设圆柱的高度为
,设圆柱的高度为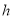
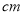 ,底面半径为
,底面半径为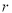
 ,且
,且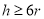 .假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为
.假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为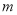 元/
元/ 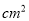 ,易拉罐上下底面的制造费用均为
,易拉罐上下底面的制造费用均为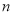 元/
元/ 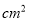 (
(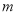 ,
, 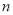 为常数,且
为常数,且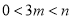 ).
).
(1)写出易拉罐的制造费用
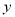 (元)关于
(元)关于 的函数表达式,并求其定义域;
的函数表达式,并求其定义域;(2)求易拉罐制造费用最低时
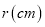 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=m-|x-1|-|x-2|,m∈R,且f(x+1)≥0的解集为[0,1].
(1)求m的值;
(2)若a,b,c,x,y,z∈R,且x2+y2+z2=a2+b2+c2=m,求证:ax+by+cz≤1.
相关试题

