【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
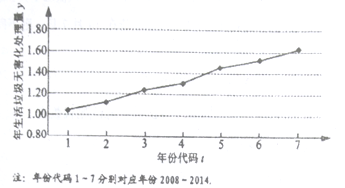
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
参考数据: ![]() ,
, ![]() ,
, 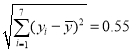 ,
, ![]() .
.
参考公式:相关系数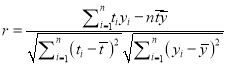
回归方程![]() 中,
中, 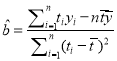 ,
, ![]() .
.
参考答案:
【答案】(1)可以用线性回归模型拟合![]() 与
与![]() 的关系;(2)1.82亿吨.
的关系;(2)1.82亿吨.
【解析】试题分析:(1)由折线图看出, ![]() 与
与![]() 之间存在较强的正相关关系,将已知数据代入相关系数方程,可得答案;(2)根据已知中的数据,求出回归系数,可得回归方程,2016年应的
之间存在较强的正相关关系,将已知数据代入相关系数方程,可得答案;(2)根据已知中的数据,求出回归系数,可得回归方程,2016年应的![]() 值为
值为![]() ,代入可预测2016年我国生活垃圾无害化处理量.
,代入可预测2016年我国生活垃圾无害化处理量.
试题解析:(1)由折线图数据和参考数据得: ![]() ,
, ![]() ,
,
所以,相关系数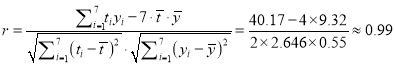
因为![]() 与
与![]() 的相关系数近似为0.99,说明
的相关系数近似为0.99,说明![]() 与
与![]() 的线性相关程度相当高,从而可以用线性回归模型拟合
的线性相关程度相当高,从而可以用线性回归模型拟合![]() 与
与![]() 的关系。
的关系。
(2)由![]() 及(1)得
及(1)得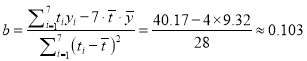 ,
, ![]() ,所以
,所以![]() 与
与![]() 的回归方程为
的回归方程为![]()
将2016年对应的![]() 代入回归方程得:
代入回归方程得: ![]() ,所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨.
,所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨.
【方法点晴】本题主要考查折线图和线性回归方程的应用,属于中档题.求回归直线方程的步骤:①依据样本数据画出散点图,确定两个变量具有线性相关关系;②计算![]() 的值;③计算回归系数
的值;③计算回归系数![]() ;④写出回归直线方程为
;④写出回归直线方程为![]() ;(2) 回归直线过样本点中心
;(2) 回归直线过样本点中心![]() 是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
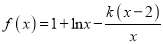 ,其中
,其中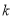 为常数.
为常数.(1)若
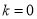 ,求曲线
,求曲线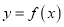 在点
在点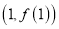 处的切线方程;
处的切线方程;(2)若
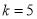 ,求
,求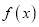 零点的个数;
零点的个数;(3)若
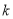 为整数,且当
为整数,且当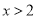 时,
时, 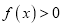 恒成立,求
恒成立,求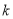 的最大值.
的最大值.(参考数据
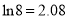 ,
, 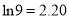 ,
, 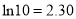 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】设A={x|x2+8x=0},B={x|x2+2(a+2)x+a2-4=0},其中a∈R.如果A∩B=B,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】判断下列函数的奇偶性.
(1)f(x)=x2-|x|+1,x∈[-1,4]; (2)f(x)=
 ;
;(3)f(x)=
 ; (4)f(x)=
; (4)f(x)=
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业拟生产一种如图所示的圆柱形易拉罐(上下底面及侧面的厚度不计).易拉罐的体积为
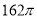
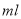 ,设圆柱的高度为
,设圆柱的高度为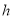
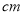 ,底面半径为
,底面半径为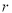
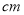 ,且
,且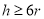 .假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为
.假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为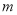 元/
元/ 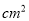 ,易拉罐上下底面的制造费用均为
,易拉罐上下底面的制造费用均为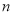 元/
元/ 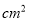 (
(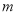 ,
, 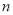 为常数,且
为常数,且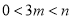 ).
).
(1)写出易拉罐的制造费用
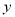 (元)关于
(元)关于 的函数表达式,并求其定义域;
的函数表达式,并求其定义域;(2)求易拉罐制造费用最低时
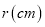 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=m-|x-1|-|x-2|,m∈R,且f(x+1)≥0的解集为[0,1].
(1)求m的值;
(2)若a,b,c,x,y,z∈R,且x2+y2+z2=a2+b2+c2=m,求证:ax+by+cz≤1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数
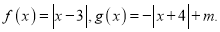
(Ⅰ)已知常数
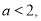 解关于
解关于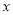 的不等式
的不等式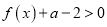 ;
;(Ⅱ)若函数
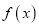 的图象恒在函数
的图象恒在函数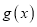 图象的上方,求实数
图象的上方,求实数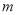 的取值范围.
的取值范围.
相关试题

