【题目】已知两点A(1,2),B(3,1)到直线l距离分别是 ![]() ,
, ![]() ﹣
﹣ ![]() ,则满足条件的直线l共有( )条.
,则满足条件的直线l共有( )条.
A.1
B.2
C.3
D.4
参考答案:
【答案】C
【解析】解:A(1,2)到直线l的距离是 ![]() ,直线是以A为圆心,
,直线是以A为圆心, ![]() 为半径的圆的切线,
为半径的圆的切线,
同理B(3,1)到直线l的距离 ![]() ﹣
﹣ ![]() ,直线是以B为圆心,
,直线是以B为圆心, ![]() 为半径的圆的切线,
为半径的圆的切线,
∴满足条件的直线l为以A为圆心, ![]() 为半径的圆和以B为圆心,
为半径的圆和以B为圆心, ![]() 为半径的圆的公切线,
为半径的圆的公切线,
∵|AB|= ![]() =
= ![]() ,
,
两个半径分别为 ![]() 和
和 ![]() ,
,
∴两圆外切,∴两圆公切线有3条
故满足条件的直线l有3条.
故选:C.
【考点精析】根据题目的已知条件,利用点到直线的距离公式的相关知识可以得到问题的答案,需要掌握点![]() 到直线
到直线![]() 的距离为:
的距离为: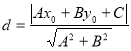 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图所示的三棱柱
 中,棱
中,棱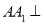 底面
底面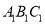 ,
, 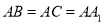 ,
, 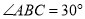 ,
, 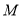 ,
, 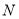 ,
, 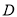 分别是
分别是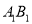 ,
, 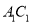 ,
, 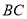 的中点.
的中点.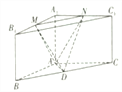
(Ⅰ)求证:
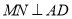 ;
;(Ⅱ)求为二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为( )
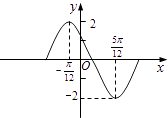
A.y=2sin(2x+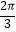 )
)
B.y=2sin(2x+ )
)
C.y=2sin( ﹣
﹣  )
)
D.y=2sin(2x﹣ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知非零向量
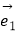 ,
, 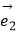 ,
,  ,
, 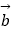 满足
满足  =2
=2 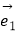 ﹣
﹣ 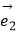 ,
, 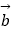 =k
=k 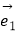 +
+ 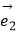 ,给出以下结论:
,给出以下结论:
①若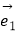 与
与 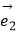 不共线,
不共线,  与
与 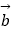 共线,则k=﹣2;
共线,则k=﹣2;
②若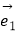 与
与 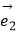 不共线,
不共线,  与
与 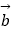 共线,则k=2;
共线,则k=2;
③存在实数k,使得 与
与 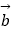 不共线,
不共线, 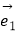 与
与 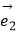 共线;
共线;
④不存在实数k,使得 与
与 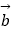 不共线,
不共线, 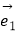 与
与 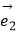 共线.
共线.
其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】用长14.8 m的钢条制作一个长方体容器的框架,如果所制的底面的一边比另一边长0.5 m,那么容器的最大容积为________m3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=sin2x+2cosx(
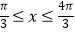 )的最大值与最小值分别为( )
)的最大值与最小值分别为( )
A.最大值 ,最小值为﹣
,最小值为﹣ 
B.最大值为 ,最小值为﹣2
,最小值为﹣2
C.最大值为2,最小值为﹣
D.最大值为2,最小值为﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了制定治理学校门口上学、放学期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查,根据从其中随机抽取的50份调查问卷,得到了如下的列联表.
同意限定区域停车
不同意限定区域停车
合计
男
18
7
25
女
12
13
25
合计
30
20
50
(1)学校计划在同意限定区域停车的家长中,按照分层抽样的方法,随机抽取5人在上学、放学期间在学校门口参与维持秩序,在随机抽取的5人中,选出2人担任召集人,求至少有一名女性的概率?
(2)已知在同意限定区域停车的12位女性家长中,有3位日常开车接送孩子,现从这12位女性家长中随机抽取3人参与维持秩序,记参与维持秩序的女性家长中,日常开车接送孩子的女性家长人数为
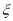 ,求
,求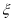 的分布列和数学期望.
的分布列和数学期望.
相关试题

