【题目】设![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,且
轴上,且![]() ,
,![]() .
.
(1)当点![]() 在
在![]() 轴上运动时,求点
轴上运动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设点![]() 是轨迹
是轨迹![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上,圆
轴上,圆![]() 内切于
内切于![]()
![]() ,求
,求![]()
![]() 的面积的最小值.
的面积的最小值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)依据题设条件直接建立坐标之间的等量关系(轨迹方程);(2)依据题设条件建立关于三角形面积公式的函数关系,最后再运用所学知识求其最小值:
试题解析:
解:(1)设![]() ,由
,由![]() ,得点
,得点![]() 为线段
为线段![]() 的中点,
的中点,
∴![]() ,
,![]() ,∴
,∴![]() ,
,![]() .
.
由![]() ,得
,得![]() .
.
所以动点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,
∴直线![]() 的方程为
的方程为![]() ,整理得:
,整理得:![]()
![]() .
.
∵圆![]() 内切于
内切于![]() ,可得
,可得![]() 与圆相切,∴
与圆相切,∴![]() ,
,
注意到![]() ,化简得:
,化简得:![]() ,
,
同理可得:![]() ,
,
因此,![]() 是方程
是方程![]() 的两个不相等的实数根.
的两个不相等的实数根.
根据根与系数的关系,化简整理可得![]()
![]()
![]() ,
,
由此可得![]() 的面积为
的面积为![]()
![]() ,
,
∴当![]() 时,即当
时,即当![]() 时,
时,![]() 的面积的最小值为8.
的面积的最小值为8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如:
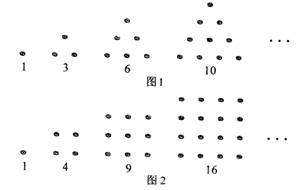
他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是( )
A. 36 B. 45 C. 99 D. 100
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一段演绎推理:“直线平行于平面,则这条直线平行于平面内所有直线;已知直线
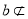 平面
平面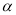 ,直线
,直线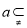 平面
平面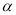 ,直线
,直线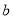 ∥平面
∥平面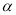 ,则直线
,则直线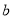 ∥直线
∥直线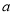 ”的结论是错误的,这是因为 ( )
”的结论是错误的,这是因为 ( )A. 大前提错误 B. 小前提错误 C. 推理形式错误 D. 非以上错误
-
科目: 来源: 题型:
查看答案和解析>>【题目】求函数
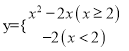 的值的程序框图如图所示.
的值的程序框图如图所示. 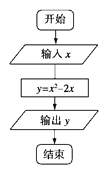
(1)指出程序框图中的错误,并写出算法;
(2)重新绘制解决该问题的程序框图,并回答下面提出的问题.
①要使输出的值为正数,输入的x的值应满足什么条件?
②要使输出的值为8,输入的x值应是多少?
③要使输出的y值最小,输入的x值应是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌手机销售商今年1,2,3月份的销售量分别是1万部,1.2万部,1.3万部,为估计以后每个月的销售量,以这三个月的销售为依据,用一个函数模拟该品牌手机的销售量y(单位:万部)与月份x之间的关系,现从二次函数
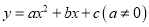 或函数
或函数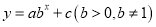 中选用一个效果好的函数行模拟,如果4月份的销售量为1.37万件,则5月份的销售量为__________万件.
中选用一个效果好的函数行模拟,如果4月份的销售量为1.37万件,则5月份的销售量为__________万件. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=
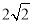 .求二面角P—BC—D余弦值的大小.
.求二面角P—BC—D余弦值的大小. 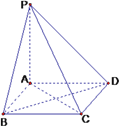
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
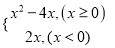 ,
,(1)画出函数y=f(x)的图象;
(2)讨论方程|f(x)|=a的解的个数.(只写明结果,无需过程)
相关试题

